Einleitung
Abituraufgabe zur analytischen Geometrie für den Grundkurs mit 30 erreichbaren Bewertungseinheiten aus Berlin 2016.
62 Minuten Erklärungen in 6 Aufgaben von Koonys Schule.
Aufgaben
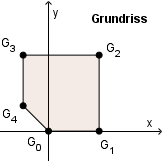
Ein Gartenhaus hat als Grundfläche ein Fünfeck mit den Eckpunkten $ \RPUNKT{G_0}{0}{0}{0} $, $ \mathrm{G_1} $, $ \RPUNKT{G_2}{2}{3}{0} $, $ \mathrm{G_3} $ und $ \RPUNKT{G_4}{-1}{1}{0} $ (s. Abbildung). Das Dach des Gartenhauses ist eine quadratische Pyramide mit den Eckpunkten $ \mathrm{D_1} $, $ \mathrm{D_2} $ und $ \mathrm{D_3} $, die in 2m Höhe genau senkrecht über $ \mathrm{G_1} $, $ \mathrm{G_2} $ und $ \mathrm{G_3} $ liegen. Der vierte Eckpunkt $ \mathrm{D_4} $ liegt nicht über einem Eckpunkt der Grundfläche.
Es gilt: 1 LE = 1 m.
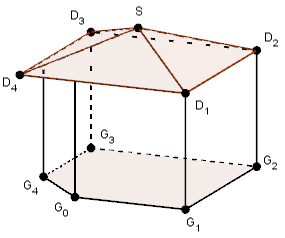
Geben Sie die Koordinaten der Punkte $ \mathrm{G_1} $, $ \mathrm{G_3} $ und $ \mathrm{D_2} $ an.
Weisen Sie nach, dass $ \RPUNKT{D_1}{2}{0}{2} $ auf der Geraden
$ g: \vec{x} = \RVEKTOR{c}{5}{-3}{0,8} + r\cdot \RVEKTOR{c}{1}{-1}{-0,4} $; $ r \in \RR $ liegt.
Die Dachspitze hat die Koordinaten $ \RPUNKT{S}{0,5}{1,5}{h} $ und liegt auch auf der
Geraden $ g $.
Berechnen Sie die Höhe $ h $ des Gartenhauses.
( Zur Kontrolle: $ \RPUNKT{S}{0,5}{1,5}{2,6} $.)
Die Firstkanten des Daches sind die vier Kanten der Pyramide, die sich im Punkt S treffen.
Berechnen Sie die Länge einer Firstkante und die Größe des Winkels, den zwei benachbarte Firstkanten an der Spitze S einschließen.
Das Dach soll mit Dachziegeln gedeckt werden.
Ein Paket Dachziegel reicht für $ 3,1\,\mathrm{m^2} $ Dachfläche.
Untersuchen Sie, ob drei Pakete ausreichend sind, um das gesamte Dach zu decken.
Zu einer bestimmten Tageszeit fällt das Sonnenlicht parallel zur Dachkante $ \overrightarrow{D_1 S} $ ein und erzeugt von $ \mathrm{D_1} $ und S einen gemeinsamen Schattenpunkt $ \mathrm{S_1} $ in der x-y-Ebene.
Berechnen Sie die Koordinaten von $ \mathrm{S_1} $.
( Zur Kontrolle: $ \RPUNKT{S_1}{7}{-5}{0} $.)
Der Schattenpunkt von $ \mathrm{D_2} $ ist der Punkt $ \RPUNKT{S_2}{7}{-2}{0} $.
Weisen Sie nach, dass die Schattenlinie $ \overrightarrow{S_1 S_2} $ parallel zur Dachkante $ \overrightarrow{D_1 D_2} $ verläuft.
Wählen Sie zwei geeignete Eckpunkte des Daches so aus, dass deren Schattenlinie senkrecht zu $ \overrightarrow{S_1 S_2} $ verläuft. Begründen Sie Ihre Wahl.
PDF zum Drucken
Lösungs-PDF
Weitere Arbeitsblätter
Felder und Kreise - GK Klausur Physik
40 min, 3 Aufgaben #6123Originale Physik Klausur für einen Grundkurs im 2. Semester aus Berlin. 39 Punkte, 90min
Ableitungsfunktion und ihre Anwendung
92 min, 12 Aufgaben #1590Aus einer Funktion macht man eine andere Funktion, die sogenannte Ableitungsfunktion. Die Aufgaben beschäftigen sich damit, wie das gemacht wird, und was man darüber hinaus mit der Ableitungsfunktion machen kann. Zum Beispiel Steigungswinkel, Schnittwinkel, Tangentengleichungen oder Berührpunkte bestimmen.
Rechnen mit Brüchen
53 min, 13 Aufgaben #066013 mal 5 Aufgaben zum Addieren, Subtrahieren, Multiplizieren und Dividieren von Brüchen. Täglich etwas machen und 2 Wochen später ist man besser. :)
Gauß Verfahren
84 min, 7 Aufgaben #1777Für lineare Gleichungssysteme mit mehr als nur zwei Gleichungen und Unbekannten gibt es einen Algorithmus mit dem man bequemer zur Lösung kommt. Dieser wird hier zunächst gezeigt und dann bei Textaufgaben zur Anwendung gebracht.
Extremwertaufgaben
72 min, 7 Aufgaben #1599Sieben verschiedene Aufgaben mit immer derselben Fragen: wann wird's maximal bzw. minimal? Sei es ein Rechteck im Kreis, der Graph einer Funktion, eine Konservendose oder eine Marmorplatte: überall muss zuerst eine Hauptbedingung und eine Nebenbedingung aufgestellt und dann zusammen in eine Funktion gepackt werden. Letztlich wird von dieser dann jedes mal der Extrempunkt bestimmt.