Einleitung
Gewinnerwartung und Wahrscheinlichkeiten bei einem bzw. zwei Würfeln.
Die Aufgaben beschäftigen sich hauptsächlich mit Baumdiagrammen und damit, aus dem Text herauszufinden was genau man zählen muss.
29 Minuten Erklärungen in 4 Aufgaben von Koonys Schule.
Aufgaben
Ein Glücksrad enthält 8 gleich große Sektoren. Vier der Sektoren sind rot, drei sind weiß und einer ist schwarz.
Laut Auszahlungsplan erhält man für Rot nichts, für Weiß 50 Cent und für Schwarz 2$\,\euro$.
Der Einsatz für ein Spiel beträgt einen halben Euro. Ist hier langfristig mit einem Gewinn für den Automatenbetreiber oder für den Spieler zu rechnen?
Ein Holzwürfel mit roter Oberfläche wird durch 6 senkrechte Schnitte in 27 gleich große Würfel zerschnitten. Diese werden dann in eine Urne gelegt. Anschließend wird aus der Urne ein Würfel gezogen. Berechnen Sie die Wahrscheinlichkeiten folgender Ereignisse:
Der gezogene Würfel hat keine rote Seite.
Der gezogene Würfel hat zwei rote Seiten.
Der gezogene Würfel hat mindestens zwei rote Seiten.
Der gezogene Würfel hat höchstens zwei rote Seiten.
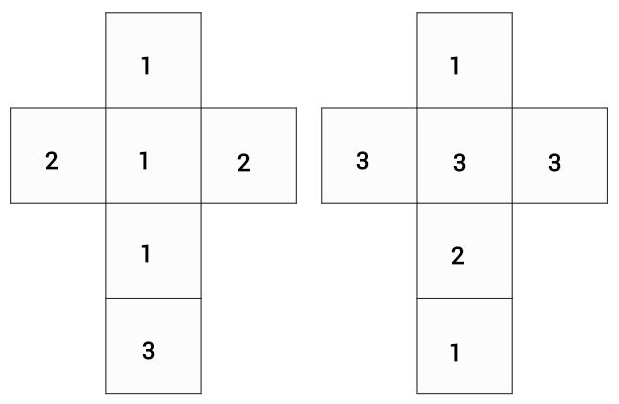
Zwei Würfel mit den abgebildeten Netzen werden gleichzeitig geworfen.
Welche Augensumme ist am wahrscheinlichsten?
Mit welcher Wahrscheinlichkeit ist die Augensumme kleiner als 5?
Wie wahrscheinlich ist ein Pasch?
Im Folgenden wird mit einem Würfel geworfen, der das abgebildete Netz mit den Ziffern 1, 2 und 6 besitzt.
(a) Der Würfel wird dreimal geworfen. Berechnen Sie die Wahrscheinlichkeiten der folgenden Ereignisse:
Die Sechs fällt genau zweimal.
Die Sechs fällt höchstens einmal.
Die Sechs fällt mindestens einmal.
$\bar{\mathrm{A}}$
$\mathrm{B} \cap \mathrm{C}$
$\mathrm{A} \cup \mathrm{B}$
(b) Herr Schneider darf den Würfel für einen Einsatz von 1€ zweimal werfen. Er hat gewonnen, wenn die Augensumme 3 beträgt oder wenn zwei Sechsen fallen. Er erhält dann 3€ Auszahlung. Ist das Spiel für Herrn Schneider günstig?
Weitere Arbeitsblätter
Klausurvorbereitung - Analysis - NRW
16 min, 3 Aufgaben #1581Beispielaufgaben für die zentralen Klausuren aus Nordrhein-Westfalen vom Schulministerium. Es wird vor allem das Verständnis der Ableitungsfunktion geprüft. Wachstumsgeschwindigkeiten, Funktionsgleichungen von Tangenten und Skizzen kommen vor.
Gartenhaus Abitur GK Berlin 2016
62 min, 6 Aufgaben #1981Abituraufgabe zur analytischen Geometrie für den Grundkurs mit 30 erreichbaren Bewertungseinheiten aus Berlin 2016.
Gleichungen in Texten
54 min, 11 Aufgaben #1337Zwei Gleichungen aufstellen und dann lösen. Immer. Zum Teil sehr knifflig!
Weidezelt Abitur GK Berlin 2016
64 min, 6 Aufgaben #1611Abituraufgabe zur Analysis für den Grundkurs mit 40 erreichbaren Bewertungseinheiten aus Berlin 2016. Neben Nullstellen, Extrempunkten und Wendepunkten sind außerdem dabei: Extremalproblem, Rekonstruktion einer quadratischen Funktion und Flächenberechnung.
Bernoulli-Ketten Anwendung
37 min, 4 Aufgaben #1701Anwendungsaufgaben zu Bernoulli-Ketten. Die ersten zwei Aufgaben fragen die grundlegenden Berechnungen ab. Die dritte ist vom Typ mindestens-mindestens und die vierte zeichnet sich durch eine äußert schwierige Aufgabenstellung aus. Ein kühler Kopf ist hier gefragt.