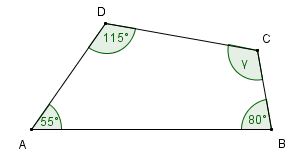
Einleitung
Aufgaben zur Konstruktion von Dreiecken mit Hilfe der Kongruenzsätze. Außerdem kommen Innenwinkelsatz, ein gleichschenkliges Trapez und die Konstruktion des Umkreises eines Dreiecks im Koordinatensystem vor.
36 Minuten Erklärungen in 5 Aufgaben von Koonys Schule.
Aufgaben
Zeichne ein Dreieck ABC mit der Seite $ c = 6\,\mathrm{cm} $ und den Winkeln $ \alpha = 53^\circ $, $ \beta = 70^\circ $.
Zeichne ein Dreieck ABC mit den Seiten $ a = 5\,\mathrm{cm} $, $ b = 7\,\mathrm{cm} $ und $ c = 9\,\mathrm{cm} $.
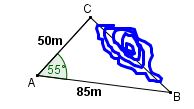
Im Gelände wurden ein Winkel und zwei Strecken gemessen.
Zeichne dazu ein Dreieck im Maßstab 1:1000 und bestimme dann durch Messen die Länge der unzugänglichen Strecke $ \overline{BC} $.
Zeichne ein gleichschenkliges Trapez mit der Grundseite $ \overline{AB} = 8\,\mathrm{cm} $, dem Winkel $ \alpha = 55^\circ $ und den Seiten $ \overline{AD} = \overline{BC} = 5\,\mathrm{cm} $.
Zeichne das Dreieck mit $ \EPUNKT{A}{3}{5} $, $ \EPUNKT{B}{10}{6} $ und $ \EPUNKT{C}{5}{19} $ im Koordinatensystem.
Bestimme durch Messen den Radius des Umkreises.
Weitere Arbeitsblätter
Lineare Gleichungssysteme lösen
62 min, 7 Aufgaben #3820Zunächst eine Vorbereitungsaufgabe. Im Anschluss Aufgaben zum Gleichsetzungsverfahren, Einsetzungsverfahren und Additionsverfahren. Danach noch Aufgaben zu den 3 möglichen Fällen: eine Lösung, keine Lösung oder unendlich vieler Lösungen. Am Ende noch Übungen bei denen auch Brüche vorkommen.
BBR - Vergleichsarbeit Mathematik
59 min, 14 Aufgaben #2508Die Vergleichende Arbeit 2015 im Fach Mathematik zum Erwerb der Berufsbildungsreife bzw. des Hauptschulabschlusses. Bearbeitungszeit: 90 Minuten. Zugelassene Hilfsmittel: Formelübersicht und wissenschaftlicher nicht grafikfähiger Standard-Taschenrechner.
Flächensätze - Vorwissen I
31 min, 7 Aufgaben #0037Verschiedene grundlegende Aufgaben zu Flächensätze. Der Umgang mit dem für das Thema wichtigen Gleichungen, Flächen- und Winkelberechnungen, sowie erste einfache Aufgaben mit dem Satz des Pythagoras kommen dran.
Lichtkunst Abitur GK Hamburg
61 min, 6 Aufgaben #1945Abituraufgabe aus der zentralen schriftlichen Abiturprüfung 2005 im Fach Mathematik aus Hamburg für den Grundkurs mit insgesamt 100 erreichbaren Punkten.
Prozent- und Zinsrechnung | MSA
18 min, 2 Aufgaben #5102Zwei originale Aufgaben aus Abschlussprüfungen für den mittleren Schulabschluss (MSA) aus Berlin. Die Rechnungen sind an sich einfach. Die Schwierigkeit besteht vor allem darin die Rechnungen aus den Textaufgaben zu extrahieren.