Klammern auflösen

Einleitung

Das Vereinfachen von Termen mit Klammern wird Stück für Stück gezeigt.
Mit dabei sind Minusklammern, das einfache und das doppelte Distributivgesetz.
Nach den Aufgaben ist man fachlich soweit sich als nächstes an die binomischen Formeln vagen zu können.

35 Minuten Erklärungen in 8 Aufgaben von Koonys Schule.

Aufgaben

Löse die Klammer auf.

$-(4+a)$

$-(b-3)$

$-(-a+7)$

$-(a+b)$

$-(x-y)$

$-(-2c-4d)$

$-(8a^2-13b^2)$

$-(-4c-5d-7e)$

$-(17x-9y-12z)$

$x-(y+z)$

$a-(b-c)$

$x-(-7+y)$

$4a-(a-b)$

$6r-(5s-8r)$

$9x-(4y+5x)$

$23c-(-9d+8c)$

$12-(4-x+y)$

$29c-(-7d-3c-5e)$

Löse die Klammer auf.

$x(1+y)$

$q(r+v)$

$k(s+t)$

$y(b+0)$

$10(3x+2y)$

$9(3a+4b)$

$2a(3y+4z)$

$9r(4s+3t)$

$4k(3m+2n)$

$20a(11b+3c)$

$22x(3y+4z)$

$10b(19e+f)$

$5(x-y)$

$2(2-y)$

$7(3-k)$

$(x-y)\cdot 7$

$(y-2)\cdot 2$

$(3-x)\cdot 8$

Löse die Klammern auf und fasse zusammen.

$3(x+2y)-3x$

$x(3+2x) + 2(x^2-x)$

$-3(a+b)-4a$

$-4(2a-5b) - 8b$

$3b-3(b-a)$

$5(x+3y) - 5x$

$(x+y)(x-y+2)$

$(a+3)(a-2)$

$(a+5)(a-2)$

$(c+b)(c-b+2)$

$(x+3)(x+4)$

$(x-2)(5-x)$

$(a+b)(a^2 - ab + b^2)$

$(a-b)(a^2-ab+b^2)$

$(2a+3b)(5a-6b+1)$

$(3x + 2y)(9x-2y-3z)$

$(5a-6b+3c)(7a-5c)$

$(10u-5v+8)(20u-13v)$

Klasse 7 Terme

PDF zum Drucken

Arbeitsblatt herunterladen

Lösungs-PDF

Lösungen freischalten

Klasse 7 Terme

Weitere Arbeitsblätter

kgV und ggT

50 min, 6 Aufgaben #0010

Primfaktorzerlegung, größter gemeinsamer Teiler und kleinstes gemeinsames Vielfaches nimmt die Hälfte des Blattes ein. Die andere Hälfte sind Anwendungsaufgaben.

Grundschule Klasse 5

Klausurvorbereitung - Analysis - NRW

15 min, 3 Aufgaben #1580

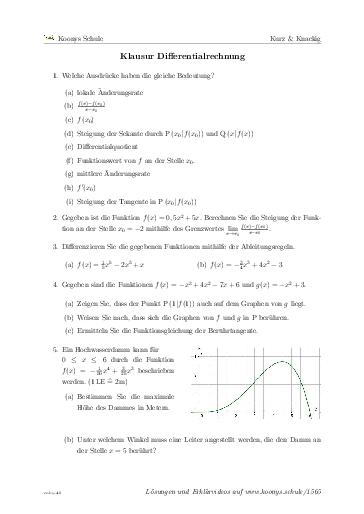
Drei kleine verschiedene Aufgaben zur Differentialrechnung. Man muss Sachen berechnen und begründete Entscheidungen geben. Dafür werden Potenzfunktionen 3. Grades mit Nullstellen, Tangenten, Ableitungen und Verschiebungen von Funktionen benutzt.

Abitur Analysis