Einleitung
Klassenarbeit über ganzrationale Funktionen mit 55 erreichbaren Punkten.
49 Minuten Erklärungen in 3 Aufgaben von Koonys Schule.
Aufgaben
Gegeben sei die Funktion $ f(x) = x^4 - 5x^2 + 6 $.
Untersuchen Sie $ f $ auf Symmetrie und dem Verhalten im Unendlichen.
Ermitteln Sie alle Achsenschnittpunkte.
Skizzieren Sie mit den Ergebnissen aus a) und b) den Graph von $ f $ im Intervall [-2,5; 2,5].
Prüfen Sie mit einer Rechnung, ob der Punkt $ \EPUNKT{P}{-1}{3} $ auf dem Graphen von $ f $ liegt.
Wie kann der Graph von $ f $ verschoben werden, damit die Funktion nur noch 2 Nullstellen hat?
Ein Möbelhaus verkauft Aufbewahrungsschachteln. Ein Set besteht aus fünf verschieden großen Schachteln, die ineinander untergebracht werden. Die Breite der Schachteln ist immer um $ 3\,\mathrm{cm} $ kürzer als die Länge $ x $ und die Höhe ist immer halb so groß wie die Länge.
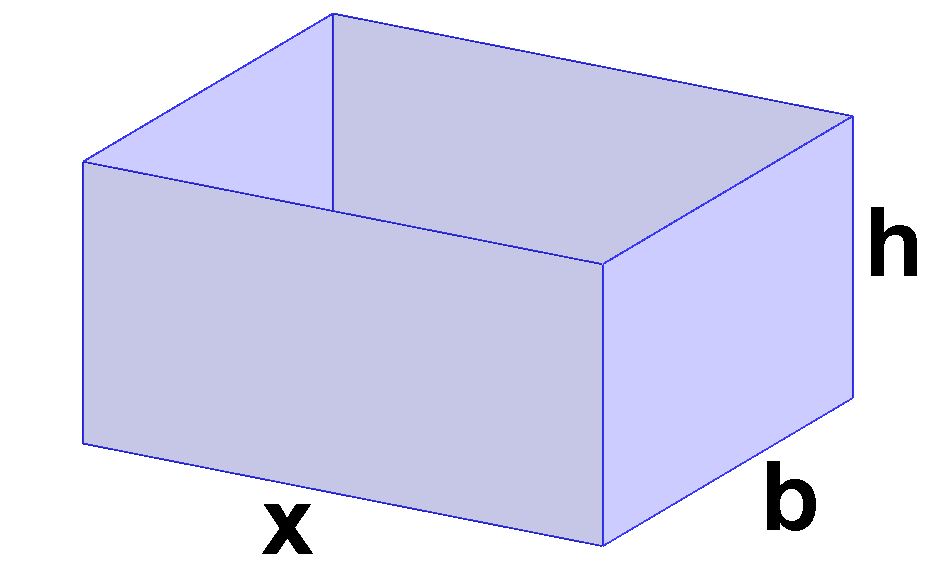
Drücken Sie die Breite $ b $ und die Höhe $ h $ in Abhängigkeit von der Länge $ x $ aus.
Zeigen Sie damit, dass die Funktion $ V(x) = \frac{1}{2}x^3 - \frac{3}{2}x^2 $ das Volumen dieser Schachteln in $ \mathrm{cm^3} $ beschreiben kann.
Welchen Grad hat $ V $? Geben Sie alle Koeffizienten an.
Skizzieren Sie den Graphen der Funktion im Intervall [-1; 4].
Ermitteln Sie dazu die Achsenschnittpunkte und verwenden Sie eine kleine Wertetabelle.
Welchen Definitionsbereich hat die Funktion bezogen auf das praktische Problem?
Markieren Sie die Stelle $ x $, ab welcher die Volumensfunktion einen Sinn ergibt und begründen Sie Ihre Meinung.
Weitere Arbeitsblätter
Hypothesentests - Signifikanztests
68 min, 5 Aufgaben #1740Aufgaben bei denen Nullhypothesen aufgestellt und mit Entscheidungsregeln angenommen oder verworfen werden. Es kommen einseitige und zweiseitige Signifikanztests vor.
Gartenhaus Abitur GK Berlin 2016
62 min, 6 Aufgaben #1981Abituraufgabe zur analytischen Geometrie für den Grundkurs mit 30 erreichbaren Bewertungseinheiten aus Berlin 2016.
Klassenarbeit - Lineare Funktionen - Geradengleichungen
28 min, 5 Aufgaben #3810Originale Klassenarbeit einer 8. Klasse aus Berlin mit 48 erreichbaren Punkten. Vorhanden sind die Zwei-Punkte-Gleichung, Punktprüfung, diverse Verständnisaufgaben zu Steigung und Achsenabschnitt und eine Anwendungsaufgabe.
Klassenarbeit binomische Formeln
33 min, 8 Aufgaben #3132Klassenarbeit einer 8. Klasse in Berlin aus dem Jahre 2015.
Textgleichungen mit Brüchen für Profis 2v3
31 min, 7 Aufgaben #1342Textaufgaben müssen gelöst werden indem man Gleichungen aufstellt bei denen Brüche vorkommen.