Einleitung
Abituraufgabe zur Analysis für den Grundkurs mit 40 erreichbaren Bewertungseinheiten aus Berlin 2016.
Neben Nullstellen, Extrempunkten und Wendepunkten sind außerdem dabei: Extremalproblem, Rekonstruktion einer quadratischen Funktion und Flächenberechnung.
64 Minuten Erklärungen in 6 Aufgaben von Koonys Schule.
Aufgaben
Weidezelte werden in der Landwirtschaft vielfältig genutzt. Sie bestehen aus einem Gerüst aus Stahlrohren, welches mit einer Plane bespannt ist, siehe Abbildung rechts.
Hersteller A nutzt für die Konstruktion der bogenförmigen Rohre als Modell den Graphen $ G_f $ der Funktion $ f(x) = -e^{0,3x^2} + 5,\, x \in \RR $. Dabei liegt die $ x $-Achse in der Höhe des Erdbodens, die $ y $-Achse verläuft durch den höchsten Punkt von $ G_f $. %, siehe Abbildung 2.
Zeigen Sie, dass $ x_{1,2} \approx \pm 2,3 $ die Nullstellen von $ f $ sind und bestimmen Sie die Koordinaten des Schnittpunktes von $ G_f $ mit der $ y $-Achse.
Geben Sie die Höhe und die Breite des Weidezeltes an ($ 1\,\mathrm{LE} = 1\,\mathrm{m} $).
Zeigen Sie rechnerisch, dass der Graph von $ G_f $ der Funktion $ f $ genau einen Extrempunkt besitzt und dieser ein Hochpunkt ist. Geben Sie die Koordinaten des Hochpunktes an und weisen Sie rechnerisch nach, dass es keine Wendepunkte gibt.
( Zur Kontrolle: $ f''(x) = e^{0,3x^2} (-0,6-0,36x^2) $)
Für die Tierhaltung nutzt man häufig für die Frontflächen Planen mit eingearbeiteten, lichtdurchlässigen Windschutznetzen. In der Abbildung rechts ist ein solches rechteckiges Netz dargestellt. Seine untere Begrenzung befindet sich in $ 2\,\mathrm{m} $ Höhe.
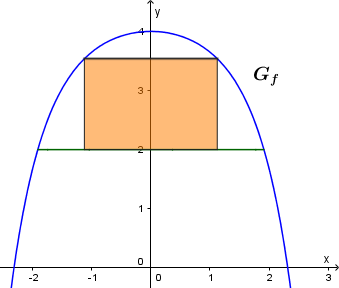
Der Flächeninhalt des Netzes soll möglichst groß sein. Stellen Sie eine Zielfunktion, also eine Funktion für den Flächeninhalt des Rechtecks, auf.
Zeigen Sie, dass bei einer Breite des Rechtecks von rund $ 2,46\,\mathrm{m} $ der Flächeninhalt extremal ist.
( Auf die Überprüfung mithilfe der 2. Ableitung wird verzichtet.)
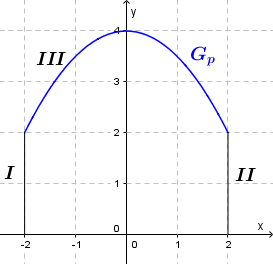
Hersteller B stellt das Gerüst der Frontfläche aus drei Stahlrohren her, sie Abbildung rechts.
Das Teilstück III wird mit dem Graphen $ G_p $ der Funktion $ p $ mit $ p(x) = ax^2 + b $ modelliert.
Entnehmen Sie der Abbildung die Koordinaten geeigneter Punkte und bestimmen Sie die Werte für $ a $ und $ b $.
( Zur Kontrolle: $ a = -0,5 $; $ b = 4 $)
Weidezelte, die für Lagerzwecke genutzt werden, werden häufig mit Planen für die Frontflächen versehen.
Ermitteln Sie die Größe der Frontfläche für das Zelt von Hersteller B.
Ein Bauer möchte im Weidezelt 10\,t Heu lagern. $ 1\,\mathrm{m^3} $ Heu hat eine Masse von 100kg.
Berechnen Sie, wie lang das Weidezelt dafür sein müsste.
PDF zum Drucken
Lösungs-PDF
Weitere Arbeitsblätter
Lineare Gleichungen
58 min, 5 Aufgaben #3738Einführung in das Umstellen von linearen Gleichungen. Die Aufgaben beginnen ganz einfach und werden dann nach und nach schwerer. Am Ende hat man gelernt: Klammern auflösen, links und rechts zusammenfassen, alles mit x auf die eine und alles ohne x auf die andere Seite. Zum Schluss noch durch die Zahl vor dem x teilen und fertig ist man.
Sinus - Kosinus - Tangens
41 min, 6 Aufgaben #7000Sinus, Kosinus und Tangens von leicht bis schwer. Zunächst Aufgaben mit den Gleichungen und all ihren Varianten. Danach Standard-Aufgaben an rechtwinkligen Dreiecken und die zweite Hälfte sind Textaufgaben bei denen das gleiche noch einmal drankommt mit dem gewissen Etwas, das anspruchsvolle Aufgaben ausmacht.
Klassenarbeit Wachstum und Zerfall
38 min, 5 Aufgaben #6551Originale Klassenarbeit zum Thema Wachstum und Zerfall aus einem E-Kurs eines 10. Jahrgangs. Es wird auf den Unterschied von linearen und exponentiellen Wachstum eingegangen, Funktionsgleichungen aufgestellt, Graphen gezeichnet und Halbwertszeiten berechnet. Außerdem kommt prozentuale Ab- und Zunahme dran, sowie das Aufstellen einer Funktionsgleichung mit zwei Punkten als Zusatzaufgabe.
Klausurvorbereitung - Analysis - NRW
16 min, 3 Aufgaben #1581Beispielaufgaben für die zentralen Klausuren aus Nordrhein-Westfalen vom Schulministerium. Es wird vor allem das Verständnis der Ableitungsfunktion geprüft. Wachstumsgeschwindigkeiten, Funktionsgleichungen von Tangenten und Skizzen kommen vor.