Einleitung
Klausurvorbereitung zu Potenzfunktionen mit Symmetrieeigenschaften, Polynomdivision, Monotonie und mittlerer Änderungsrate.
35 Minuten Erklärungen in 6 Aufgaben von Koonys Schule.
Aufgaben
Gegeben ist ein Polynom mit $f(x) = 1,25x^5-3x^3+1,1x$.
Liegt P(1 $\vert$ -1,5) auf dem Graphen?
Berechnen Sie alle Nullstellen des Polynoms.
Zeichnen Sie das Polynom in ein Koordinatensystem. Bestimmen Sie dazu auch jeweils einen Punkt zwischen den Nullstellen.
Geben Sie für die entsprechenden Intervalle die Monotonie an.
Gegeben ist das Polynom $g(x) = x^8 - 16x^6 - 5x-7$.
Prüfen Sie jeweils durch Polynomdivision, ob -4 und 1 Nullstellen der Funktion sind und begründen Sie ihre Entscheidung.
Könnte diese Funktion noch mehr Nullstellen haben? Begründen Sie ihre Entscheidung.
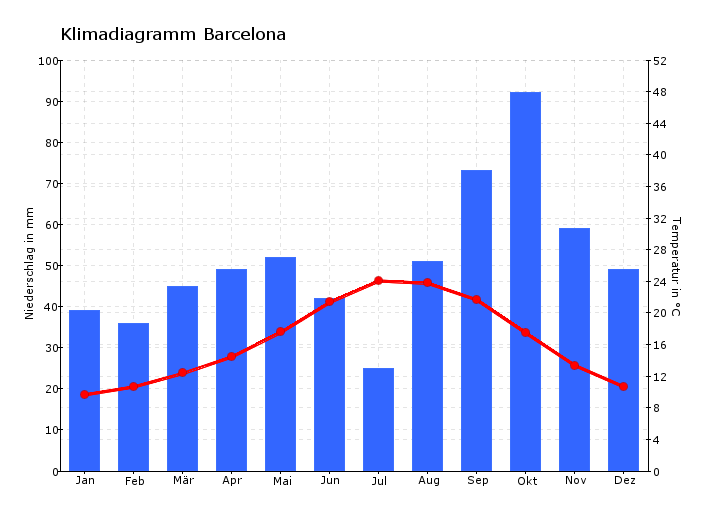
Betrachtungen zum Wetter.
Berechnen Sie für die Monate Mai bis Juli und Juli bis Oktober jeweils die mittlere Änderungsrate des Niederschlags mit dem Differenzenquotienten.
Machen Sie 2 bis 3 Aussagen zur Niederschlagsmenge auf der Grundlage ihrer Berechnungen.
Weitere Arbeitsblätter
Hypothesentests - Signifikanztests
68 min, 5 Aufgaben #1740Aufgaben bei denen Nullhypothesen aufgestellt und mit Entscheidungsregeln angenommen oder verworfen werden. Es kommen einseitige und zweiseitige Signifikanztests vor.
Binomische Formeln
89 min, 11 Aufgaben #3120Alles rund um die binomischen Formeln. Voraussetzung ist das Auflösen von doppelten Klammern (doppeltes Distributivgesetz). Darauf aufbauend wird auf das Vereinfachen von Termen eingegangen bei denen die binomischen Formeln von einfach bis schwer zur Anwendung kommen. Danach wird der Spieß umgedreht und Terme mit den binomischen Formeln faktorisiert. Krönender Abschluss bilden Gleichungen bei denen man ... *trommelwirbel* ... binomische Formeln braucht.
kgV und ggT
50 min, 6 Aufgaben #0010Primfaktorzerlegung, größter gemeinsamer Teiler und kleinstes gemeinsames Vielfaches nimmt die Hälfte des Blattes ein. Die andere Hälfte sind Anwendungsaufgaben.
Berechnungen an Körpern
62 min, 6 Aufgaben #9598Zunächst müssen Skizzen von Zylinder, Kegel, Pyramide und Kugel angefertigt werden. Anschließend gibt es einfache Aufgaben zu Oberfläche und Volumen wobei nur gegebene Werte in entsprechende Formeln eingesetzt werden müssen. Danach variieren die gegebenen Werte, sodass die Formeln umgestellt werden müssen.
Wurzelterme vereinfachen ohne Taschenrechner
41 min, 13 Aufgaben #0990Viele verschiedene Aufgaben zum Zusammenfassen von Wurzeltermen. Dabei werden neben den Wurzelgesetzen auch binomische Formeln benötigt.






