Einleitung
Die Strahlensätze werden zunächst an klassischen Aufgaben mit gegebener Skizze gezeigt und im Anschluss an Textaufgaben gefestigt.
27 Minuten Erklärungen in 3 Aufgaben von Koonys Schule.
Aufgaben
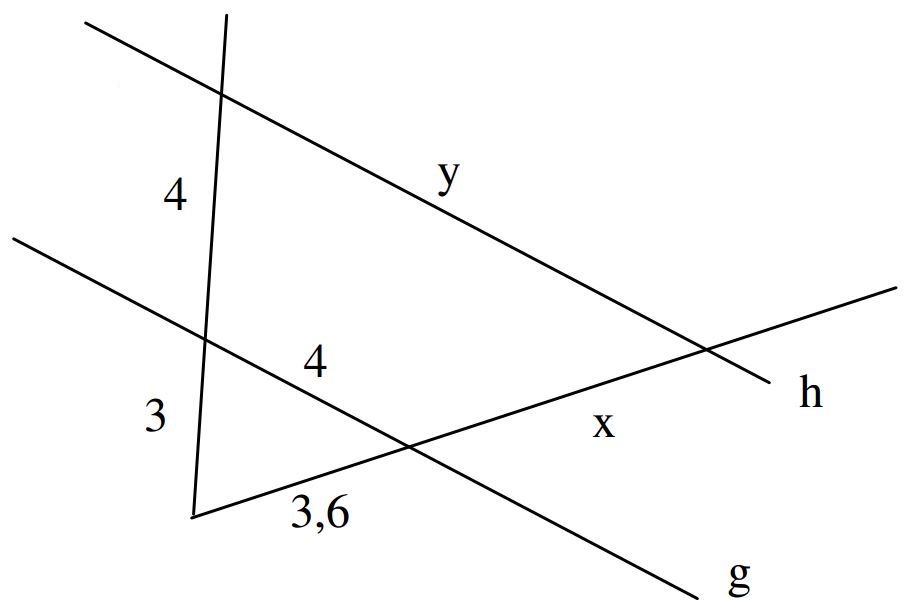
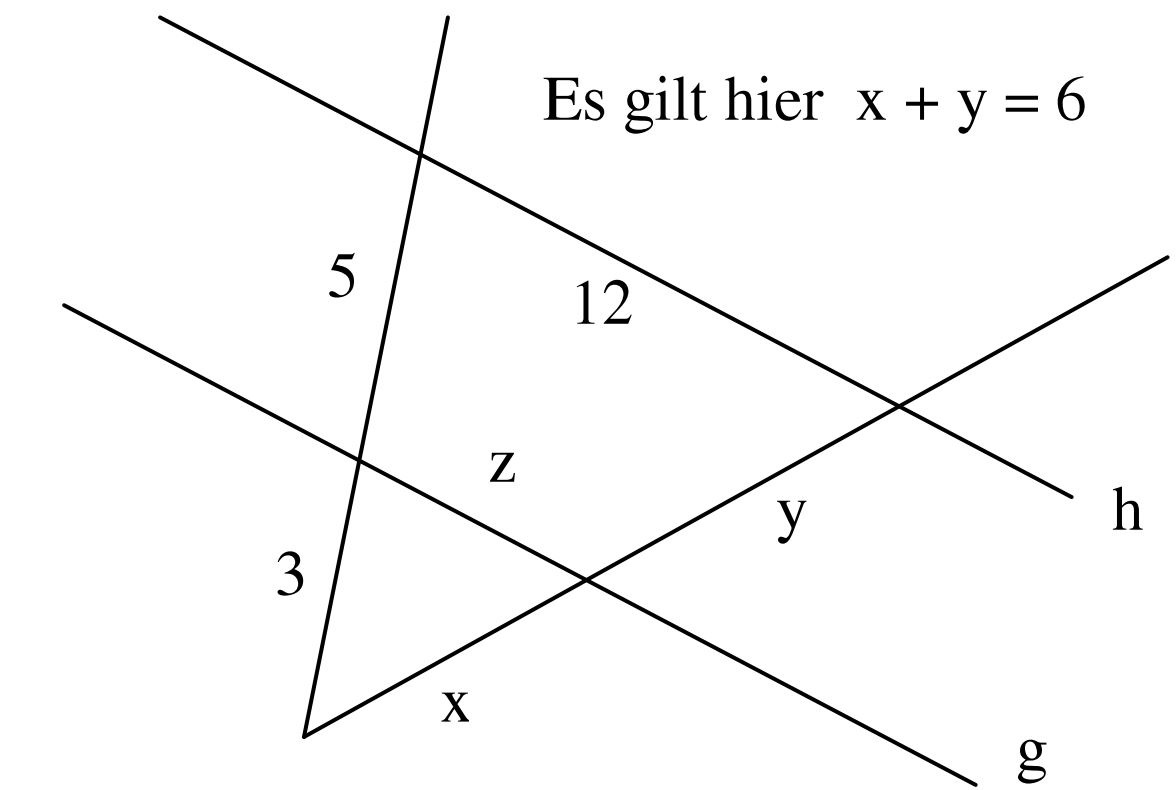
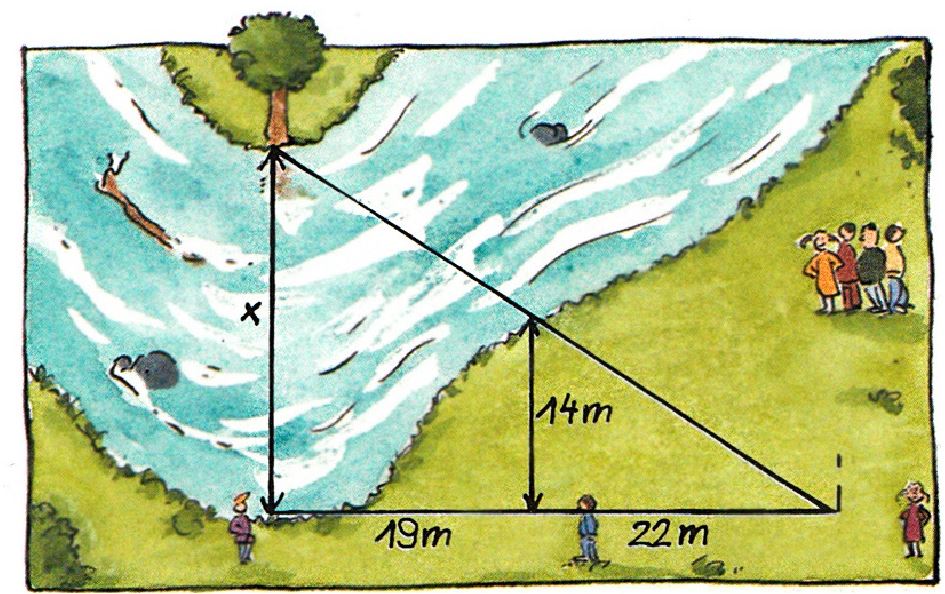
Auf einem Wandertag haben die Schülerinnen und Schüler in Gruppen die Breite x des Flusses bestimmt.
Auf welches Ergebnis sind sie mit ihren Messergebnissen gekommen?
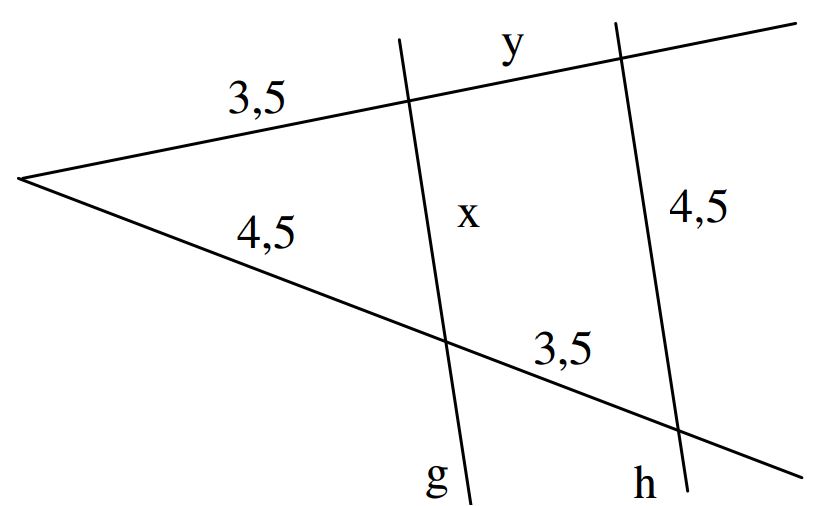
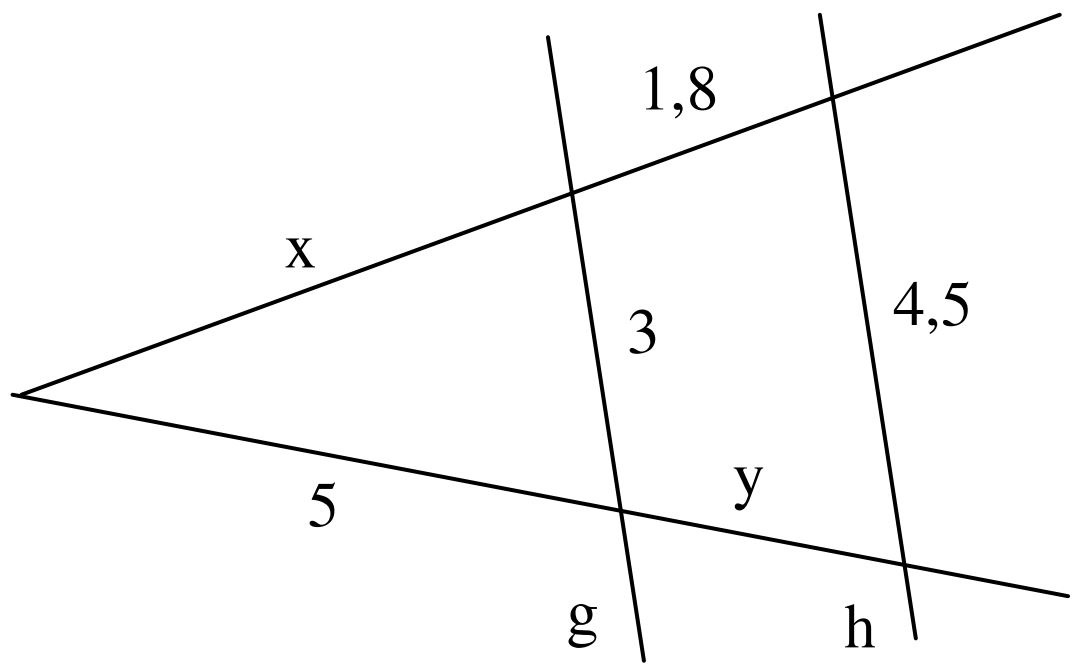
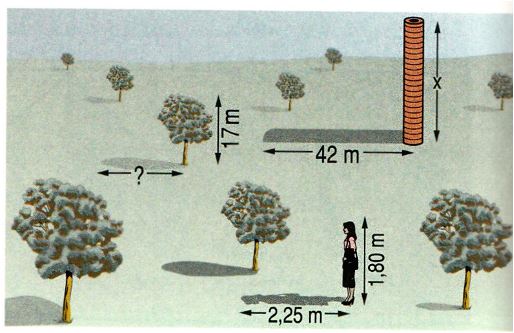
Ein Schornstein wirft einen Schatten von 42m Länge. Zur gleichen Zeit ist der Schatten einer 1,80m großen Schülerin 2,25m lang.
Wie hoch ist der Schornstein?
Wie lang ist zur gleichen Zeit der Schatten eines 17m hohen Baumes neben dem Schornstein?
Wie hoch wäre der Schornstein, wenn der Schatten des Mädchens 15cm länger wäre?
Schätze zunächst.
Alle Erklärungen sind auch in einer
PDF zum Drucken
Lösungs-PDF
Weitere Arbeitsblätter
Klausur - Grundkurs - 2. Semester
42 min, 3 Aufgaben #1660Originale Grundkurs Klausur aus Berlin eines 2. Semesters. Der Hauptteil ist die Kurvendiskussion einer e-Funktion. Wendetangente, Stammfunktion und Flächeninhalt inklusive. Die andere Hälfte beinhaltet Integralrechnung mit Parametern und ein paar kombinatorische Aufgaben.
Klassenarbeit Terme und Gleichungen
27 min, 4 Aufgaben #3749Klassenarbeit einer 8. Klasse auf einem Berliner Gymnasium. Es müssen Terme vereinfacht und Gleichungen gelöst werden. Dabei müssen Klammern aufgelöst, binomische Formeln angewendet und Gleichungen aus Texten aufgestellt werden.
Mathematische Kompetenzen - Zufall
15 min, 6 Aufgaben #0008Ein Sachverhalt aus dem Themengebiet Daten und Zufall (Leitidee 5) wird in verschiedene Aufgaben gepackt, die jeweils einen Schwerpunkt bezüglich der mathematischen Kompetenzen besitzen.
Strahlensätze **
54 min, 6 Aufgaben #4182Drei Schenkel, verdrehte Skizzen, Erbsen und der Mond sowie Bergspitzen. Das Prinzip ist das Gleiche, aber die Schwierigkeit ist doch um einiges größer als sonst. Das nächste Level an Strahlensatzaufgaben sozusagen.
Anteile, Bruchteile, Ausgangsgröße und Einheiten
48 min, 6 Aufgaben #0506Wenn es um Anteile geht gibt es drei grundlegende Aufgabentypen. Jeweils muss der Groschen dabei fallen, damit man es auch wirklich versteht und weitere mathematische Konzepte erschließbar werden. Passend zu der Thematik beschäftigt sich die andere Hälfte des Arbeitsblattes mit der Umrechnung von Einheiten.