Einleitung
Vier Aufgabentypen zu Sinus, Kosinus und Tangens an nicht rechtwinkligen Dreiecken.
Bei den Aufgaben hat man zwar beliebige Dreiecke vorliegen, aber kommt ganz ohne Sinussatz und Kosinussatz aus.
59 Minuten Erklärungen in 5 Aufgaben von Koonys Schule.
Aufgaben
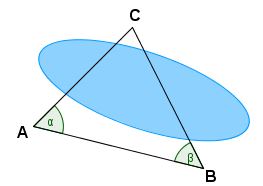
Die Punkte A und B sind vom Punkt C durch unzugängliches Gelände getrennt.
Man misst $ \overline{AB} = 6\,\mathrm{km} $, $ \alpha = 75° $ und $ \beta = 42° $.
Wie weit sind A und B von C entfernt?
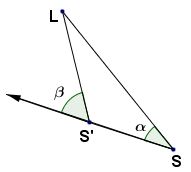
Ein Schiff S peilt einen Leuchtturm L bei festem Kurs unter einem Winkel $ \alpha $ an und nach $ 8\,\mathrm{km} $ noch einmal unter dem Winkel $ \beta $.
Gemessen wurde $ \alpha = 40° $ und $ \beta = 60° $.
Wie groß waren zu den Zeitpunkten die Entfernungen zum Leuchtturm?
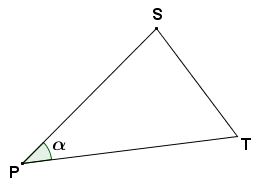
Vom Punkt P in einem Bergwerk werden 2 Stollen unter einem Winkel $ \alpha $ geradlinig in den Berg getrieben. Der Vortrieb zum Endpunkt S ist $ 1,5\,\mathrm{km} $ und der Vortrieb zum Endpunkt T $ 2\,\mathrm{km} $ lang. Der Winkel $ \alpha $ hat eine Größe von 55°.
Wie lang wäre ein geradliniger Verbindungsstollen von S nach T?
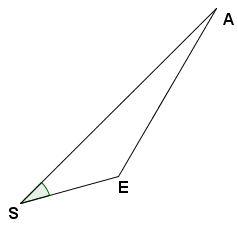
Vom Punkt S beträgt die Entfernung zum geplanten Eingang E eines linearen Tunnels durch einen Berg $ 2\,\mathrm{km} $. Der Ausgang A ist vom Punkt S $ 8\,\mathrm{km} $ entfernt.
Der Winkel zwischen $ \overline{\mathrm{SE}} $ und $ \overline{\mathrm{SA}} $ beträgt 25°.
Wie lang wird der Tunnel?
PDF zum Drucken
Lösungs-PDF
Weitere Arbeitsblätter
Teilweises Wurzelziehen - Rationalmachen des Nenners
52 min, 11 Aufgaben #0992Aufgaben zum teilweisen, auch partiellen, Wurzelziehen mit Zahlen, Variablen und Faktorisieren. Einfache Aufgaben zum Rationalmachen des Nenners.
Textgleichungen mit Brüchen für Profis 1v3
39 min, 8 Aufgaben #1341Textaufgaben müssen gelöst werden indem man Gleichungen aufstellt bei denen Brüche vorkommen.
Lichtkunst Abitur GK Hamburg
61 min, 6 Aufgaben #1945Abituraufgabe aus der zentralen schriftlichen Abiturprüfung 2005 im Fach Mathematik aus Hamburg für den Grundkurs mit insgesamt 100 erreichbaren Punkten.
Ikarus Abitur GK Berlin 2016
64 min, 6 Aufgaben #1980Abituraufgabe zur analytischen Geometrie für den Grundkurs mit 30 erreichbaren Bewertungseinheiten aus Berlin 2016.