Einleitung
Schritt für Schritt werden die verschiedenen Ableitungsregeln bei e-Funktionen gezeigt und es gibt Aufgaben mit Kombinationen dieser Regeln (Konstantenregel, Faktorregel, Produktregel, Kettenregel).
Das Arbeitsblatt endet mit einer typischen Kurvendiskussion über eine e-Funktion.
69 Minuten Erklärungen in 7 Aufgaben von Koonys Schule.
Aufgaben
Konstantenregel: $ f(x) = e^x + a \Rightarrow f'(x) = e^x $
$ f(x) = e^x + 3 $
$ f(x) = e^x - 6^3 $
$ f(x) = e^x + \sqrt{\frac{e^2}{2}} $
Faktorregel: $ f(x) = a\cdot e^x \Rightarrow f'(x) = a\cdot e^x $
$ f(x) = 4e^x $
$ f(x) = e^3 e^x $
$ f(x) = \sqrt{\frac{e^2}{-0,5}} e^x $
Beliebige Basis: $ f(x) = a^x \Rightarrow f'(x) = \ln(a)\cdot a^x $
$ f(x) = 4^x $
$ f(x) = 0,4^x $
$ f(x) = (4^{-1})^x $
Produktregel: $ f(x) = u(x)\cdot e^x \Rightarrow f'(x) = u'(x)\cdot e^x + u(x)\cdot e^x $
$ f(x) = xe^x $
$ f(x) = \frac{2}{x} e^x $
$ f(x) = \left(\frac{2}{x} + \frac{2}{\sqrt{x}}\right)e^x $
Kettenregel: $ f(x) = e^{u(x)} \Rightarrow f'(x) = u'(x) \cdot e^{u(x)} $
$ f(x) = e^{2x} $
$ f(x) = e^{x^2} $
$ f(x) = e^{\sqrt{x}} $
Bilden Sie jeweils die 1. Ableitung durch die Kombination mehrerer Regeln.
$ f(x) = x e^x - 6e^{2x}$
$ f(x) = x^2 e^x - 6e^{\sqrt{x}} $
$ f(x) = \frac{3}{e^x} - e^{\sqrt{x + x^2}} $
$ f(x) = \frac{e^{\sqrt{x^2 - \frac{4}{x}}}}{(x-2)^2} $
Kurvendiskussion
Gegeben sei die Funktion $ f(x) = 3e^x\cdot (e^x - 1) $.
Stellen Sie das Verhalten im Unendlichen fest.
Ermitteln Sie die Nullstellen, Extrem- und Wendepunkte.
Skizzieren Sie die Funktion für ein geeignetes Intervall.
An welcher Stelle hat die Funktion die Steigung 1,5?
Alle Erklärungen sind auch in einer
PDF zum Drucken
Lösungs-PDF
Weitere Arbeitsblätter
Extremwertaufgaben
80 min, 8 Aufgaben #1597Acht verschiedene Aufgaben mit immer derselben Fragen: wann wird's maximal bzw. minimal? Sei es mit einem Schiff, in einer Spielzeugfabrik, auf einer Wiese oder als Motorradfahrer: überall muss zuerst eine Hauptbedingung und eine Nebenbedingung aufgestellt und dann zusammen in eine Funktion gepackt werden. Letztlich wird von dieser dann jedes mal der Extrempunkt bestimmt.
Klassenarbeit binomische Formeln
33 min, 8 Aufgaben #3132Klassenarbeit einer 8. Klasse in Berlin aus dem Jahre 2015.
Arbeit - ganzrationale Funktionen
49 min, 3 Aufgaben #1520Klassenarbeit über ganzrationale Funktionen mit 55 erreichbaren Punkten.
Abschlussarbeit Klasse 9 mit Taschenrechner
42 min, 6 Aufgaben #2853Aufgaben quer durch die 9. Klasse. Statistiken, lineare Gleichungen, Funktionen, Textgleichungen, Strahlensätze, Prozentrechnung und Flächeninhalten. Auch als Vorbereitung auf den mittleren Schulabschluss (MSA) geeignet.
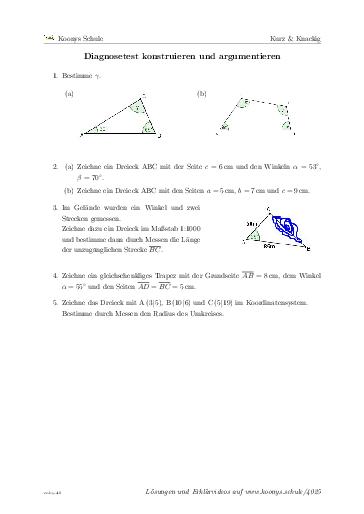
Diagnosetest konstruieren und argumentieren
36 min, 5 Aufgaben #4025Aufgaben zur Konstruktion von Dreiecken mit Hilfe der Kongruenzsätze. Außerdem kommen Innenwinkelsatz, ein gleichschenkliges Trapez und die Konstruktion des Umkreises eines Dreiecks im Koordinatensystem vor.