Einleitung
Originale Arbeit einer 9. Klasse mit 60 möglichen Punkten ohne Taschenrechner zur Wurzelrechnung.
27 Minuten Erklärungen in 9 Aufgaben von Koonys Schule.
Aufgaben
Fasse so weit wie möglich zusammen.
$3\sqrt{2} + 2\sqrt{3} - \sqrt{2} + \sqrt{3} - 8\sqrt{2}$
$5\sqrt{a} - (7\sqrt{b} + 3\sqrt{a}) -\sqrt{a}$
Vereinfache mit Hilfe der Wurzelgesetze.
$\sqrt{6xy^3}\cdot\sqrt{24x^3y}$
$\frac{\sqrt{x^2y^3}}{\sqrt{y}}$
Vereinfache durch teilweises Wurzelziehen. Fasse dann so weit wie möglich zusammen.
$3\sqrt{169x} - 4\sqrt{225y} + 9\sqrt{196x} - 7\sqrt{400y}$
Vereinfache soweit wie möglich. (binomische Formeln)
$\left(\sqrt{5} + \sqrt{11}\right)^2$
$\left(\sqrt{6} - \sqrt{24}\right)^2$
$\left(\sqrt{12} + 3\right)\cdot\left(\sqrt{12} - 3\right)$
$\sqrt{25x^2 - 80xy + 64y^2}$
Mache den Nenner rational. (Beseitige die Wurzeln im Nenner.)
$\frac{8}{\sqrt{14}}$
$\frac{\sqrt{18}}{\sqrt{3} + \sqrt{2}}$
PDF zum Drucken
Lösungs-PDF
Weitere Arbeitsblätter
Klassenarbeit - Lineare Funktionen - Geradengleichungen
28 min, 5 Aufgaben #3810Originale Klassenarbeit einer 8. Klasse aus Berlin mit 48 erreichbaren Punkten. Vorhanden sind die Zwei-Punkte-Gleichung, Punktprüfung, diverse Verständnisaufgaben zu Steigung und Achsenabschnitt und eine Anwendungsaufgabe.
Wochenübung - besondere quadratische Gleichungen
89 min, 6 Aufgaben #0065Für sechs Tage gibt es täglich 4 Aufgaben. Eine Bruchgleichung, eine biquadratische Gleichung, eine Gleichung 3. Grades ohne Absolutglied und eine zum Knobeln.
Terme vereinfachen
35 min, 4 Aufgaben #2832Übungen zum Vereinfachen von Termen durch die vier Grundrechenarten: Addition, Subtraktion, Multiplikation und Division. Unter anderem müssen gleichartige Glieder zusammengefasst und Klammern aufgelöst werden.
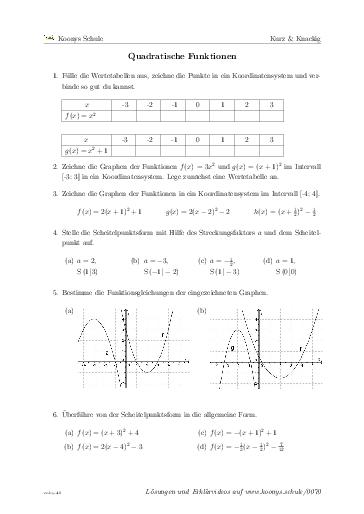
Arbeit - quadratische Funktionen
39 min, 4 Aufgaben #0069Eine originale Arbeit mit 46 erreichbaren Punkten zum Thema quadratische Funktionen. Mit dabei: Linearfaktor, Satz von Vieta, Scheitelpunktsform, Optimierungsproblem und Imbiss Bronko.
Diagnosetest konstruieren und argumentieren
36 min, 5 Aufgaben #4025Aufgaben zur Konstruktion von Dreiecken mit Hilfe der Kongruenzsätze. Außerdem kommen Innenwinkelsatz, ein gleichschenkliges Trapez und die Konstruktion des Umkreises eines Dreiecks im Koordinatensystem vor.