Einleitung
Schritt für Schritt werden die verschiedenen Ableitungsregeln bei e-Funktionen gezeigt und es gibt Aufgaben mit Kombinationen dieser Regeln (Konstantenregel, Faktorregel, Produktregel, Kettenregel).
Das Arbeitsblatt endet mit einer typischen Kurvendiskussion über eine e-Funktion.
69 Minuten Erklärungen in 7 Aufgaben von Koonys Schule.
Aufgaben
Konstantenregel: $ f(x) = e^x + a \Rightarrow f'(x) = e^x $
$ f(x) = e^x + 3 $
$ f(x) = e^x - 6^3 $
$ f(x) = e^x + \sqrt{\frac{e^2}{2}} $
Faktorregel: $ f(x) = a\cdot e^x \Rightarrow f'(x) = a\cdot e^x $
$ f(x) = 4e^x $
$ f(x) = e^3 e^x $
$ f(x) = \sqrt{\frac{e^2}{-0,5}} e^x $
Beliebige Basis: $ f(x) = a^x \Rightarrow f'(x) = \ln(a)\cdot a^x $
$ f(x) = 4^x $
$ f(x) = 0,4^x $
$ f(x) = (4^{-1})^x $
Produktregel: $ f(x) = u(x)\cdot e^x \Rightarrow f'(x) = u'(x)\cdot e^x + u(x)\cdot e^x $
$ f(x) = xe^x $
$ f(x) = \frac{2}{x} e^x $
$ f(x) = \left(\frac{2}{x} + \frac{2}{\sqrt{x}}\right)e^x $
Kettenregel: $ f(x) = e^{u(x)} \Rightarrow f'(x) = u'(x) \cdot e^{u(x)} $
$ f(x) = e^{2x} $
$ f(x) = e^{x^2} $
$ f(x) = e^{\sqrt{x}} $
Bilden Sie jeweils die 1. Ableitung durch die Kombination mehrerer Regeln.
$ f(x) = x e^x - 6e^{2x}$
$ f(x) = x^2 e^x - 6e^{\sqrt{x}} $
$ f(x) = \frac{3}{e^x} - e^{\sqrt{x + x^2}} $
$ f(x) = \frac{e^{\sqrt{x^2 - \frac{4}{x}}}}{(x-2)^2} $
Kurvendiskussion
Gegeben sei die Funktion $ f(x) = 3e^x\cdot (e^x - 1) $.
Stellen Sie das Verhalten im Unendlichen fest.
Ermitteln Sie die Nullstellen, Extrem- und Wendepunkte.
Skizzieren Sie die Funktion für ein geeignetes Intervall.
An welcher Stelle hat die Funktion die Steigung 1,5?
Alle Erklärungen sind auch in einer
PDF zum Drucken
Lösungs-PDF
Weitere Arbeitsblätter
Smartphones Abitur GK Berlin 2016
44 min, 6 Aufgaben #1991Abituraufgabe zur analytischen Geometrie für den Grundkurs mit 30 erreichbaren Bewertungseinheiten aus Berlin 2016.
Abschlussarbeit Klasse 9 ohne Taschenrechner
42 min, 11 Aufgaben #2851Aufgaben quer durch die 9. Klasse für Profis. Potenzrechnung, Terme, Gleichungen umstellen, Geometrie, Brüche, Maßstäbe, Funktionen und Kombinatorik. Alles ohne Taschenrechner! Auch als Vorbereitung auf den mittleren Schulabschluss (MSA) geeignet.
Aus 3 mach 4 - Abitur GK Berlin 2008
23 min, 5 Aufgaben #1987Original Abiturprüfung aus Berlin für den Grundkurs mit einem Glücksspielautomat. Mit dabei war die Kombinatorik, stochastische Unabhängigkeit, Bernoulli-Ketten, mindestens-mindestens Aufgabe und ein Hypothesentest.
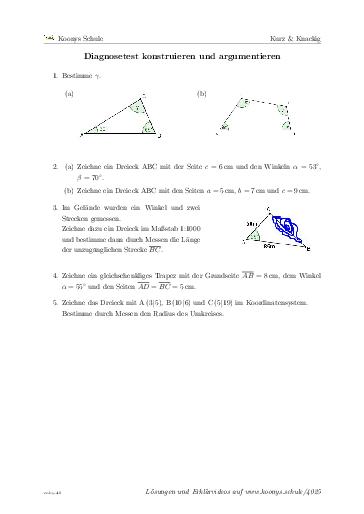
Diagnosetest konstruieren und argumentieren
36 min, 5 Aufgaben #4025Aufgaben zur Konstruktion von Dreiecken mit Hilfe der Kongruenzsätze. Außerdem kommen Innenwinkelsatz, ein gleichschenkliges Trapez und die Konstruktion des Umkreises eines Dreiecks im Koordinatensystem vor.