Einleitung
Abituraufgabe zur analytischen Geometrie für den Grundkurs mit 30 erreichbaren Bewertungseinheiten aus Berlin 2016.
44 Minuten Erklärungen in 6 Aufgaben von Koonys Schule.
Aufgaben
Smartphones sind mit unterschiedlichen Betriebssystemen ausgestattet.
In Deutschland nutzen von den Smartphone-Besitzern
70 % das Betriebssystem A,
20 % das Betriebssystem B,
10 % andere Betriebssysteme.
Im Folgenden werden entsprechend die Bezeichnungen A-Phone und B-Phone verwendet.
In einer Straßenbahn sitzen 20 Personen.
Jede dieser Personen besitzt genau ein Smartphone.
Genau 12 von ihnen besitzen ein A-Phone.
Weniger als 2 von ihnen besitzen ein B-Phone.
Jede der 20 Personen besitzt entweder ein A-Phone oder ein B-Phone.
Berechnen Sie die Wahrscheinlichkeiten der folgenden Ereignisse:
Genau 12 von ihnen besitzen ein A-Phone.
Weniger als 2 von ihnen besitzen ein B-Phone.
Jede der 20 Personen besitzt entweder ein A-Phone oder ein B-Phone.
Tatsächlich sitzen in der Straßenbahn genau 14 Personen, die ein A-Phone besitzen.
Vier der 20 Personen steigen aus.
Bestimmen Sie die Wahrscheinlichkeit der folgenden Ereignisse.
Die ersten beiden Aussteigenden besitzen ein A-Phone, der dritte nicht.
Der erste Aussteigende besitzt ein A-Phone und von den anderen 3 noch genau einer.
Von den 16 Personen, die in der Straßenbahn geblieben sind, besitzen genau 11 ein A-Phone.
In einem Kursprojekt sollen Schülerinnen und Schüler die Verbreitung unterschiedlicher Betriebssysteme in Deutschland untersuchen. Sie befragen Personen nach der Art des Betriebssystems, welches Sie in ihrem Smartphone nutzen.
Berechnen Sie, wie viele Personen mindestens befragt werden müssen, um mit einer Wahrscheinlichkeit von mindestens 95 % mindestens einen B-Phone-Nutzer zu finden.
An einer Haltestelle warten $ n $ Personen, die alle ein Smartphone besitzen.
Ein Schüler behauptet, dass die Wahrscheinlichkeit dafür, dass alle Wartenden ein A- oder B-Phone nutzen, mindestens 50 % beträgt.
Untersuchen Sie, für welche Anzahlen $ n $ diese Behauptung zutrifft.
PDF zum Drucken
Lösungs-PDF
Weitere Arbeitsblätter
Übung zu Bewegungen im magnetischem Feld
54 min, 4 Aufgaben #6116Aufgaben mit Elektronen und Protonen, die sich in Magnetfeldern im Kreis bewegen oder abgelenkt werden. Die Lorentzkraft wird dabei der Zentripetalkraft oder der elektrischen Kraft gleichgesetzt.
Übersicht e-Funktionen ableiten
69 min, 7 Aufgaben #6600Schritt für Schritt werden die verschiedenen Ableitungsregeln bei e-Funktionen gezeigt und es gibt Aufgaben mit Kombinationen dieser Regeln (Konstantenregel, Faktorregel, Produktregel, Kettenregel). Das Arbeitsblatt endet mit einer typischen Kurvendiskussion über eine e-Funktion.
Übungsaufgaben zur Wahrscheinlichkeitsrechnung
29 min, 4 Aufgaben #1656Gewinnerwartung und Wahrscheinlichkeiten bei einem bzw. zwei Würfeln. Die Aufgaben beschäftigen sich hauptsächlich mit Baumdiagrammen und damit, aus dem Text herauszufinden was genau man zählen muss.
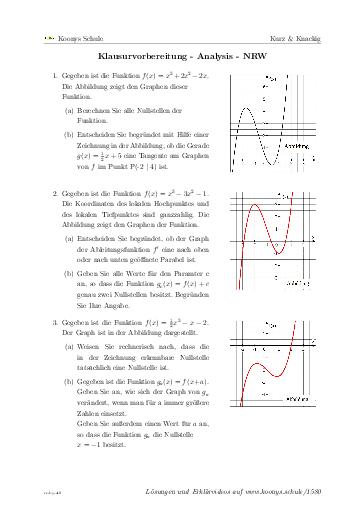
Klausurvorbereitung - Analysis - NRW
15 min, 3 Aufgaben #1580Drei kleine verschiedene Aufgaben zur Differentialrechnung. Man muss Sachen berechnen und begründete Entscheidungen geben. Dafür werden Potenzfunktionen 3. Grades mit Nullstellen, Tangenten, Ableitungen und Verschiebungen von Funktionen benutzt.
Klassenarbeit Terme und Gleichungen
26 min, 5 Aufgaben #3750Klassenarbeit einer 8. Klasse auf einem Berliner Gymnasium. Es müssen Terme vereinfacht und Gleichungen gelöst werden. Dabei müssen Klammern aufgelöst, binomische Formeln angewendet und Gleichungen aus Texten aufgestellt werden.