Einleitung
Übungsblatt der Hochschule Kaiserslautern, University of Applied Sciences, zum Thema Vektoren.
127 Minuten Erklärungen in 10 Aufgaben von Koonys Schule.
Aufgaben
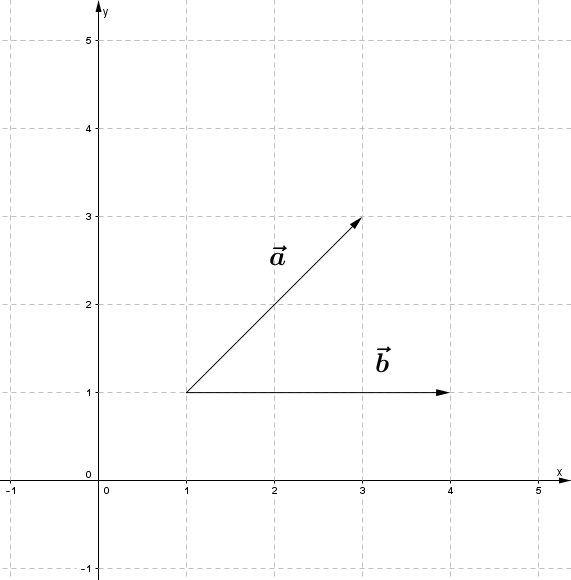
Im nebenstehenden Bild sind zwei Repräsentanten der Vektoren $ \vec{a} $ und $ \vec{b} $ dargestellt.
Berechnen Sie das Skalarprodukt
aus den Längen von $ \vec{a} $ und $ \vec{b} $ und dem Winkel $ \varphi = \angle(\vec{a},\vec{b}) $.
aus den Koordinaten von $ \vec{a} $ und $ \vec{b} $.
Ein Parallelogramm hat die Eckpunkte $ \RPUNKT{A}{1}{3}{6} $, $ \RPUNKT{B}{3}{7}{3} $, $ \RPUNKT{C}{8}{7}{5} $ und D.
Bestimmen Sie die Koordinaten von D und den Schnittpunkt der Diagonalen.
Berechnen Sie die Innenwinkel des Parallelogramms, sowie den Winkel, unter dem sich die Diagonalen schneiden.
Berechnen Sie den Flächeninhalt des Parallelogramms.
Untersuchen Sie, ob die Punkte $ \RPUNKT{G}{\frac{13}{4}}{5}{5} $ und $ \RPUNKT{H}{4}{-1}{5} $ innerhalb des Parallelogramms liegen.
Ein Viereck hat die Eckpunkte $ \RPUNKT{A}{2}{0}{3} $, $ \RPUNKT{B}{4}{4}{4} $, $ \RPUNKT{C}{11}{7}{9} $ und $ \RPUNKT{D}{9}{3}{8} $.
Untersuchen Sie, ob das Viereck ABCD ein Parallelogramm ist.
Zwei Vektoren $ \vec{a} $ und $ \vec{b} $ haben die Koordinaten $ \vec{a} = \RVEKTOR{c}{3}{1}{2} $ und $ \vec{b} = \RVEKTOR{c}{-1}{2}{1} $.
Berechnen Sie
das Vektorprodukt $ \vec{a}\times\vec{b} $.
das Skalarprodukt $ \vec{a}\cdot\vec{b} $.
Die Punkte $ \RPUNKT{A}{8}{4}{0} $, $ \RPUNKT{B}{0}{6}{2} $, $ \RPUNKT{C}{0}{0}{8} $ und $ \RPUNKT{D}{8}{-1}{5} $ sind Eckpunkte eines Vierecks.
Stellen Sie das Viereck in einem räumlichen Koordinatensystem dar.
Weisen Sie nach, dass das Dreieck ABC rechtwinklig und gleichschenklig ist.
Berechnen Sie die Größe des Flächeninhalts des Vierecks ABCD.
PDF zum Drucken
Lösungs-PDF
Weitere Arbeitsblätter
Lernkontrolle Potenzen
39 min, 8 Aufgaben #0994Verschiedene Aufgaben zu Zehnerpotenzen. Zwei Textaufgaben inklusive. Bei den zwei letzten Aufgaben müssen mit Hilfe von Potenzgesetzen Terme vereinfacht werden.
Mathematische Kompetenzen - Zufall
15 min, 6 Aufgaben #0008Ein Sachverhalt aus dem Themengebiet Daten und Zufall (Leitidee 5) wird in verschiedene Aufgaben gepackt, die jeweils einen Schwerpunkt bezüglich der mathematischen Kompetenzen besitzen.
Prozent- und Zinsrechnung | MSA
18 min, 2 Aufgaben #5102Zwei originale Aufgaben aus Abschlussprüfungen für den mittleren Schulabschluss (MSA) aus Berlin. Die Rechnungen sind an sich einfach. Die Schwierigkeit besteht vor allem darin die Rechnungen aus den Textaufgaben zu extrahieren.
Gauß Verfahren
84 min, 7 Aufgaben #1777Für lineare Gleichungssysteme mit mehr als nur zwei Gleichungen und Unbekannten gibt es einen Algorithmus mit dem man bequemer zur Lösung kommt. Dieser wird hier zunächst gezeigt und dann bei Textaufgaben zur Anwendung gebracht.
Übungsaufgaben zur Stochastik
30 min, 6 Aufgaben #1654Die ersten fünf Aufgaben fragen danach, wie viele Elemente oder Möglichkeiten es gibt, und sind damit klassische Aufgaben zu Abzählverfahren (Kombinatorik). Die letzte Aufgabe beschäftigt sich mit Baumdiagrammen und Bernoulli-Ketten.