Einleitung
Originaler Test mit 40 erreichbaren Punkten.
31 Minuten Erklärungen in 4 Aufgaben von Koonys Schule.
Aufgaben
Gegeben ist die Funktion $ f(x) = -x^2 - x + 6 $.
Geben Sie $ f $ in Scheitelpunktsform und in ihrer Linearfaktordarstellung an.
Notieren Sie alle Achsenschnittpunkte und den Scheitelpunkt.
Zeichnen Sie den Graph von $ f $ in das Koordinatensystem.

Eine Gerade $ g $ verläuft durch die Punkte $ \EPUNKT{P_1}{-1}{4} $ und $ \EPUNKT{P_2}{1}{8} $.
Ermitteln Sie die Steigung und den y-Achsenabschnitt von $ g $. Geben Sie dann die Funktionsgleichung an.
Untersuchen Sie die Lage der Geraden $ g $ zur Parabel $ f $ aus Aufgabe 1 rechnerisch. Um was für eine Gerade handelt es sich?
Zeichnen Sie $ g $ in dasselbe Koordinatensystem aus Aufgabe 1 und überprüfen Sie Ihre Ergebnisse anhand der Graphen.
Gegeben ist die Funktion $ f(x) = \frac{1}{2}x^4 + 2x^3 - x+1 $.
Wie nennt man diese Form der Darstellung? Geben Sie den Grad von $ f $ an und nennen Sie alle Koeffizienten.
Geben Sie für die Potenzfunktion $ p(x) = -x^3 $ alle charakteristischen Punkte an.
Nennen Sie wesentliche Eigenschaften und beschreiben Sie den Verlauf des Graphen von $ p $.
Weitere Arbeitsblätter
Klassenarbeit Terme und Gleichungen
26 min, 5 Aufgaben #3750Klassenarbeit einer 8. Klasse auf einem Berliner Gymnasium. Es müssen Terme vereinfacht und Gleichungen gelöst werden. Dabei müssen Klammern aufgelöst, binomische Formeln angewendet und Gleichungen aus Texten aufgestellt werden.
Gauß Verfahren
84 min, 7 Aufgaben #1777Für lineare Gleichungssysteme mit mehr als nur zwei Gleichungen und Unbekannten gibt es einen Algorithmus mit dem man bequemer zur Lösung kommt. Dieser wird hier zunächst gezeigt und dann bei Textaufgaben zur Anwendung gebracht.
Glücksrad mit Urne - Übungsaufgabe Stochastik LK
21 min, 6 Aufgaben #1710Eine Übungsaufgabe, die Urne und Glücksrad kombiniert. Nebst Baumdiagrammen, Bernoulli und der summierten Binomialverteilung werden auch Gewinnerwartung und Prozentrechnung beim Kreis benötigt.
Sinus - Kosinus - Tangens
41 min, 6 Aufgaben #7000Sinus, Kosinus und Tangens von leicht bis schwer. Zunächst Aufgaben mit den Gleichungen und all ihren Varianten. Danach Standard-Aufgaben an rechtwinkligen Dreiecken und die zweite Hälfte sind Textaufgaben bei denen das gleiche noch einmal drankommt mit dem gewissen Etwas, das anspruchsvolle Aufgaben ausmacht.
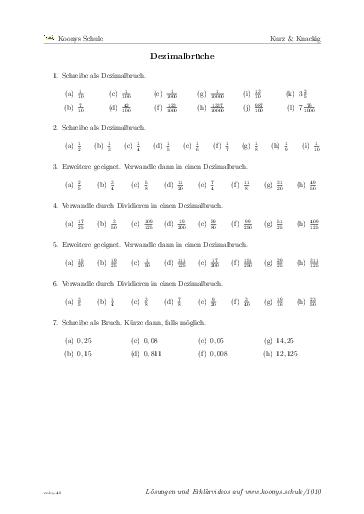
Dezimalbrüche
85 min, 7 Aufgaben #1010In verschiedenen Aufgaben werden gebrochene Zahlen zwischen Dezimalzahlen und echten Brüchen hin und her umgewandelt.