Einleitung
In verschiedenen Anwendungsaufgaben müssen die Kreisformeln genutzt werden. Umstellen der Formeln, Kreisausschnitte, Prozent- und Geschwindigkeitsrechnung müssen darüber hinaus angewendet werden.
59 Minuten Erklärungen in 5 Aufgaben von Koonys Schule.
Aufgaben
Leite eine Formel für den Umfang eines Kreises bei gegebener Fläche her.
Wieviel mal größer wird der Umfang eines Kreises, wenn man die Fläche von $2\,\mathrm{m^2}$ auf $8\,\mathrm{m^2}$ vergrößert?
Aus einem quadratischem Blech mit dem Umfang $1,50\,\mathrm{m}$ soll ein möglichst großes kreisförmiges Blechstück herausgeschnitten werden.
Berechne den Radius und die Fläche des kreisförmigen Blechstücks.
Berechne die Fläche des Restes.
Wie hoch ist der Abfall in Prozent?
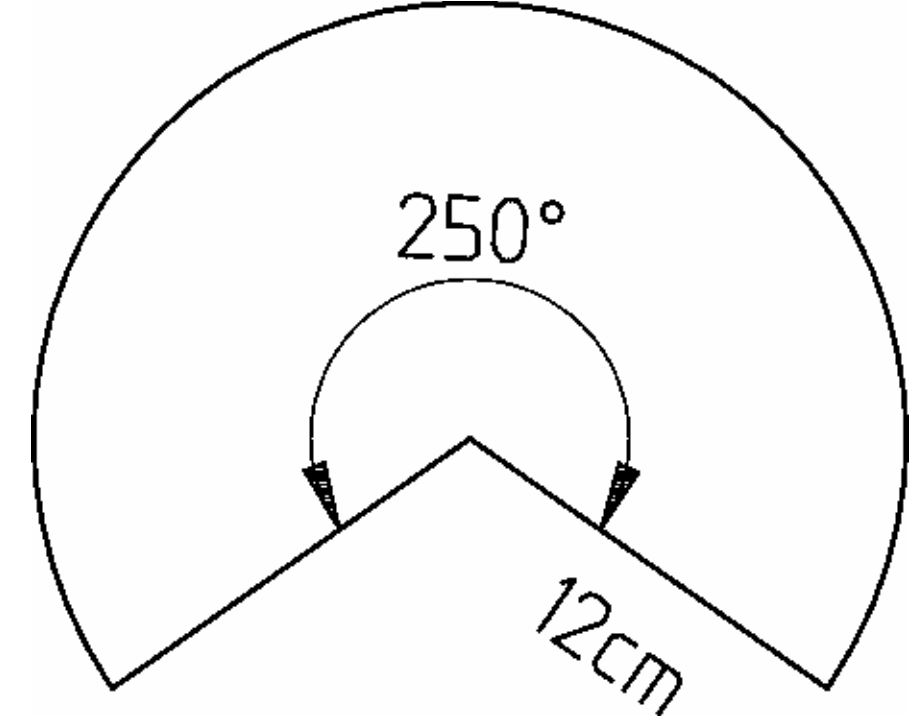
Aus dem nebenstehendem Kreissektor wird ein Kegel geformt.
Wie groß sind Mantelfläche und Volumen?
Ein Zebra läuft mit sechs Kilometern in der Stunde durch die Steppe.
Welche Kreisfläche könnte es in acht Stunden umrunden (gleichmäßige Geschwindigkeit vorausgesetzt)?
Die Räder eines Fahrrads haben einen Durchmesser von 80cm.
Wie viele Umdrehungen macht das Rad auf einem km? Runde das Ergebnis auf ganze Umdrehungen.
Da die Räder nicht genügend aufgepumpt sind, verringert sich der Durchmesser um 2cm. Wie viele Umdrehungen braucht das Rad jetzt pro km?
Der Kilometerzähler des Rades ist auf die Radgröße von 80cm geeicht. Du bist nach dem Kilometerzähler 40km gefahren. Welche Strecke hast du wirklich zurückgelegt, wenn am Durchmesser der Räder durch schlechtes Aufpumpen 2cm fehlen?
Wie viele km müsstest du nach dem Kilometerzähler fahren, um mit dem schlecht aufgepumpten Fahrrad tatsächlich 40km zurückzulegen?
Weitere Arbeitsblätter
Lernkontrolle Wahrscheinlichkeitsrechnung
36 min, 4 Aufgaben #7392Typische Aufgaben der Wahrscheinlichkeitsrechnung für die Sekundarstufe. Mit dabei sind Ergebnismengen, Baumdiagramme und Gewinnerwartung. Natürlich auch Urnen, viele Kugeln und Lotterielose.
Binomische Formeln
89 min, 11 Aufgaben #3120Alles rund um die binomischen Formeln. Voraussetzung ist das Auflösen von doppelten Klammern (doppeltes Distributivgesetz). Darauf aufbauend wird auf das Vereinfachen von Termen eingegangen bei denen die binomischen Formeln von einfach bis schwer zur Anwendung kommen. Danach wird der Spieß umgedreht und Terme mit den binomischen Formeln faktorisiert. Krönender Abschluss bilden Gleichungen bei denen man ... *trommelwirbel* ... binomische Formeln braucht.
Übungen zu kombinatorischen Abzählverfahren
29 min, 8 Aufgaben #1648Ob mit oder ohne Reihenfolge und mit oder ohne Wiederholung: die Frage, die sich stellt, ist immer die gleiche: wie viele Möglichkeiten gibt es? Bei den Aufgaben kommt man noch häufig durch Abzählen zur Lösung.
Terme addieren und subtrahieren
43 min, 8 Aufgaben #2828Terme vereinfachen indem man gleichartige Glieder zusammenfasst und ggf. vorher noch ein paar Klammern auflöst. Auch müssen Terme aufgestellt und Zahlenmauern gelöst werden.
Klausurvorbereitung - Analysis - NRW
15 min, 3 Aufgaben #1580Drei kleine verschiedene Aufgaben zur Differentialrechnung. Man muss Sachen berechnen und begründete Entscheidungen geben. Dafür werden Potenzfunktionen 3. Grades mit Nullstellen, Tangenten, Ableitungen und Verschiebungen von Funktionen benutzt.