Einleitung
Abituraufgabe zur analytischen Geometrie für den Grundkurs mit 30 erreichbaren Bewertungseinheiten aus Berlin 2016.
46 Minuten Erklärungen in 8 Aufgaben von Koonys Schule.
Aufgaben
Nina und Max treffen sich zu einem Spiel mit 32 Karten. 16 der 32 Karten zeigen auf einer Seite die Farbe rot, die anderen 16 zeigen die Farbe Schwarz. Anhand ihrer Rückseiten sind die Karten nicht zu unterscheiden.
Zunächst mischt Nina und nimmt 3 Karten vom Stapel, in dem die 32 Karten verdeckt liegen.
Berechnen Sie die Wahrscheinlichkeit dafür, dass die 3 Karten die gleiche Farbe haben.
Berechnen Sie die Wahrscheinlichkeit dafür, dass wenigstens eine rote Karte unter den 3 gezogenen Karten ist.
Alle 32 Karten werden neu gemischt, das Spiel beginnt. Das Spiel besteht aus $ n $ Runden.
In jeder Runde zieht ein Spieler eine Karte, deckt sie auf, steckt sie wieder in den Stapel und mischt ihn.
Zieht der Spielpartner danach die gleiche Farbe, hat er die erste Runde gewonnen.
Nach jeder Runde wird die Reihenfolge der Ziehenden gewechselt.
Begründen Sie, dass für die Wahrscheinlichkeit des Ereignisses
E: Wer zuerst zieht, gewinnt die Runde gilt: P($ E $) = 0,5.
Es werden 10 Runden gespielt.
Berechnen Sie die Wahrscheinlichkeit der folgenden Ereignisse:
Nina gewinnt die ersten 3 Runden.
Nina gewinnt mindestens 5 der 10 Runden.
Nina gewinnt die erste Runde und von den restlichen neun noch genau 5.
Nachdem Nina und Max 15 Runden gespielt haben, sieht der Zettel mit den Ergebnissen wie rechts abgebildet aus. Sie beschließen, noch genau 5 Runden zu machen. Wer dann mehr als die Hälfte der 20 Runden gewonnen hat, ist Gewinner des Spiels.
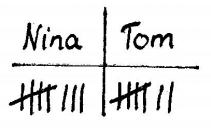
Berechnen Sie die Wahrscheinlichkeit dafür, dass Max noch genau 4 der 5 Runden gewinnt.
Berechnen Sie die Wahrscheinlichkeit dafür, dass Nina das Spiel gewinnt.
Am nächsten Tag wird das Spiel verändert. Nun wird eine Karte gezogen und offen auf den Tisch gelegt. Wer als Zweiter zieht und eine Karte derselben Farbe gezogen hat, der hat die Runde gewonnen. Andernfalls hat gewonnen, wer die erste Karte gezogen hat.
Das Spiel besteht aus $ m $ Runden.
Begründen Sie anhand einer geeigneten Rechnung, dass diese Spielvariante nur dann fair ist, wenn die Anzahl $ m $ der Runden gerade ist.
PDF zum Drucken
Lösungs-PDF
Weitere Arbeitsblätter
Abzählverfahren
35 min, 6 Aufgaben #1651Verschiedene Aufgaben mit Würfel-Würfen und Zahlen mit ihren Ziffern. Gefragt ist jedes mal nach der Wahrscheinlichkeit, dass ein bestimmtes Ereignis passiert. Schwierigkeit liegt darin herauszufinden, was die Anzahl aller Ergebnisse und die Anzahl der günstigen Ergebnisse ist.
Übungsaufgaben zur Stochastik
30 min, 6 Aufgaben #1654Die ersten fünf Aufgaben fragen danach, wie viele Elemente oder Möglichkeiten es gibt, und sind damit klassische Aufgaben zu Abzählverfahren (Kombinatorik). Die letzte Aufgabe beschäftigt sich mit Baumdiagrammen und Bernoulli-Ketten.
Aus 3 mach 4 - Abitur GK Berlin 2008
23 min, 5 Aufgaben #1987Original Abiturprüfung aus Berlin für den Grundkurs mit einem Glücksspielautomat. Mit dabei war die Kombinatorik, stochastische Unabhängigkeit, Bernoulli-Ketten, mindestens-mindestens Aufgabe und ein Hypothesentest.
Terme addieren und subtrahieren
43 min, 8 Aufgaben #2828Terme vereinfachen indem man gleichartige Glieder zusammenfasst und ggf. vorher noch ein paar Klammern auflöst. Auch müssen Terme aufgestellt und Zahlenmauern gelöst werden.
Terme und Gleichungen - Arbeit
0 min, 9 Aufgaben #TUGAA41 Punkte Klassenarbeit für die 8. Klasse: Umfassendes Arbeitsblatt zu Termen und Gleichungen. Enthält Aufgaben zur Vereinfachung von Termen, Multiplikation, Anwendung der binomischen Formeln, Klammerauflösung, Bestimmung von Lösungsmengen und Sachaufgaben. Perfekt zur Überprüfung und Vertiefung algebraischer Fähigkeiten.






