Einleitung
Sieben verschiedene Aufgaben mit immer derselben Fragen: wann wird's maximal bzw. minimal?
Sei es ein Rechteck im Kreis, der Graph einer Funktion, eine Konservendose oder eine Marmorplatte: überall muss zuerst eine Hauptbedingung und eine Nebenbedingung aufgestellt und dann zusammen in eine Funktion gepackt werden. Letztlich wird von dieser dann jedes mal der Extrempunkt bestimmt.
72 Minuten Erklärungen in 7 Aufgaben von Koonys Schule.
Aufgaben
Die Zahl 12 soll so in zwei Summanden zerlegt werden, dass
die Summe der Quadrate der gesuchten Summanden möglichst klein wird;
ihr Produkt maximal wird;
die Summe aus dem Quadrat des einen Summanden und dem doppelten Quadrat des anderen Summanden minimal wird.
Bestimme die Seitenlängen und den Umfang desjenigen Rechtecks, das in einem Kreis mit dem Radius $ r = 3\sqrt{2}\,\mathrm{cm}$ einbeschrieben ist und maximalen Umfang $u$ hat.
Der Graph der Funktion $ f(x) = \sqrt{r^2 - x^2} $ mit $ r > 0$ und die x-Achse schließen eine Fläche ein. In diese Fläche wird ein Rechteck so gelegt, dass die Seiten jeweils parallel zu den Koordinatenachsen verlaufen.
Bestimme die Koordinaten der Eckpunkte des Rechtecks, dessen Flächeninhalt maximal ist und gib den maximalen Flächeninhalt an.
Es sei $ f(x) = (x-3)^2 + 2,5 $ für $ 0\le x \le 3 $. Betrachtet werden sollen alle achsenparallele Rechtecke mit dem Ursprung als einen Eckpunkt und einem Punkt des Graphen als gegenüberliegenden Eckpunkt.
Berechne die Koordinaten der Eckpunkte des Rechteckes, dessen Flächeninhalt maximal ist und gib den Flächeninhalt an.
Eine Konservendose von 1 Liter Inhalt soll so bemessen sein, dass möglichst wenig Material zur Herstellung gebraucht wird. Berechnen Sie Durchmesser und Höhe.
Ein oben offenes Gefäß besteht aus dem Mantel eines Zylinders mit angesetzter Halbkugel. Die gesamte Außenfläche des Gefäßes habe einen Flächeninhalt von $ 400\,\mathrm{cm}^2 $.
Bestimme den Radius und die Höhe so, dass das Volumen des Körpers maximal wird.
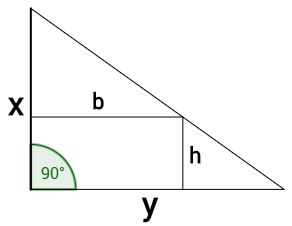
Aus einer dreieckigen Marmorplatte mit x = 50cm und y = 70cm soll ein rechteckiges Stück herausgeschnitten werden.
Berechne Breite und Höhe, sodass der Flächeninhalt des Rechteckes maximal ist.
Alle Erklärungen sind auch in einer
PDF zum Drucken
Lösungs-PDF
Weitere Arbeitsblätter
Berechnungen an Körpern
62 min, 6 Aufgaben #9598Zunächst müssen Skizzen von Zylinder, Kegel, Pyramide und Kugel angefertigt werden. Anschließend gibt es einfache Aufgaben zu Oberfläche und Volumen wobei nur gegebene Werte in entsprechende Formeln eingesetzt werden müssen. Danach variieren die gegebenen Werte, sodass die Formeln umgestellt werden müssen.
Studienkolleg Vektoren, SS 2017
127 min, 10 Aufgaben #1818Übungsblatt der Hochschule Kaiserslautern, University of Applied Sciences, zum Thema Vektoren.
Quadratische Funktionen
53 min, 6 Aufgaben #0070Eine Einführung in quadratische Funktionen. Begonnen wird mit der Normalparabel. Das wird weiter und weiter ausgebaut bis hin zur Scheitelpunktsform und beendet mit der Übung diese in die allgemeine Form zu überführen. Ausblick könnte die quadratische Ergänzung sein.
Klammern auflösen
51 min, 5 Aufgaben #3335Aufgaben zum Vereinfachen von Termen mit Klammern. Zunächst Terme mit Minusklammern, dann welche mit doppelten Klammern (doppeltes Distributivgesetz). Am Ende, so ganz nebenbei, die binomischen Formeln und der ganze Spaß rückwärts: das Ausklammern.
Teilweises Wurzelziehen - Rationalmachen des Nenners
52 min, 11 Aufgaben #0992Aufgaben zum teilweisen, auch partiellen, Wurzelziehen mit Zahlen, Variablen und Faktorisieren. Einfache Aufgaben zum Rationalmachen des Nenners.