Einleitung
Viele verschiedene Aufgaben zum Zusammenfassen von Wurzeltermen. Dabei werden neben den Wurzelgesetzen auch binomische Formeln benötigt.
41 Minuten Erklärungen in 13 Aufgaben von Koonys Schule.
Aufgaben
$3\sqrt{2} + 4\sqrt{2}$
$9\sqrt{3} - 7\sqrt{3}$
$12\sqrt{11} + 5\sqrt{11}$
$4\sqrt{6} + 3\sqrt{6} - 2\sqrt{6}$
$4\sqrt{x} + 3\sqrt{x}$
$14\sqrt{x} - 9\sqrt{x}$
$2\sqrt{a}+3\sqrt{a} - \sqrt{a}$
$3\sqrt{x} - 2\sqrt{x} + 4\sqrt{x}$
$4\sqrt{3} + 2\sqrt{5} - 2\sqrt{3} + 8\sqrt{5}$
$6\sqrt{7} + 5\sqrt{2} - 3\sqrt{2} + 8\sqrt{7}$
$4\sqrt{11} + 3\sqrt{13} - \sqrt{11}- 4\sqrt{11}$
$9\sqrt{17} + 3\sqrt{21} - 14\sqrt{21} + 6\sqrt{17}$
$5\sqrt{x} + 2\sqrt{y} - 3\sqrt{x} - 4\sqrt{y}$
$5\sqrt{a} + 6\sqrt{b} - 8\sqrt{b} + 7\sqrt{a}$
$8\sqrt{2x} - 7\sqrt{3y} + 5\sqrt{2x} - 3\sqrt{3y}$
$12\sqrt{p} - 3\sqrt{3q} - 5\sqrt{3q} - 6\sqrt{p}$
$5\sqrt{a}- ( 7\sqrt{b} + 3\sqrt{a}) - \sqrt{a}$
$5\sqrt{x} - (3\sqrt{x} + \sqrt{y}) - (\sqrt{x} + 2\sqrt{y})$
$-(\sqrt{2a} + 7\sqrt{3b}) - (4\sqrt{2a} - 3\sqrt{3b})$
$\sqrt{x} - (2\sqrt{y} + 3\sqrt{z}) - (\sqrt{x} - \sqrt{y} - \sqrt{z})$
$\sqrt{5a}\cdot\sqrt{20a}$
$\sqrt{2a^2}\cdot\sqrt{18a^2}$
$\sqrt{72k} \cdot\sqrt{2k}$
$\sqrt{12x}\cdot\sqrt{3x^3}$
$\sqrt{\frac{1}{2}m}\cdot\sqrt{32m}$
$\sqrt{\frac{3}{4}x}\cdot\sqrt{\frac{3}{16}x}$
$\sqrt{0,18a}\cdot\sqrt{2a}$
$\sqrt{20y}\cdot\sqrt{1,8y}$
$\frac{\sqrt{72}}{\sqrt{2}}$
$\frac{\sqrt{125}}{\sqrt{5}}$
$\frac{\sqrt{20}}{\sqrt{\frac{4}{5}}}$
$\frac{\sqrt{\frac{1}{3}}}{\sqrt{\frac{3}{4}}}$
$\frac{\sqrt{x^3}}{\sqrt{x}}$
$\frac{\sqrt{\frac{a^2}{b}}}{\sqrt{b}}$
$\frac{\sqrt{xy}}{\sqrt{\frac{x}{y}}}$
$\frac{\sqrt{x^2 y^3}}{\sqrt{y}}$
$(\sqrt{12} + \sqrt{3})\sqrt{3}$
$\sqrt{2}(\sqrt{18} + \sqrt{32})$
$\sqrt{5}(\sqrt{5} + \sqrt{125})$
$\sqrt{6}(\sqrt{54} + \sqrt{6})$
$(\sqrt{32x} + \sqrt{8x})\sqrt{0,5x}$
$\sqrt{0,2a}\cdot(\sqrt{5a} - \sqrt{80a})$
$(3 + \sqrt{5})(3-\sqrt{5})$
$(\sqrt{8} - \sqrt{3})(\sqrt{8} + \sqrt{3})$
$(\sqrt{2} + \sqrt{7})(\sqrt{2} - \sqrt{7})$
$(\sqrt{12} + 3)(\sqrt{12} - 3)$
$(\sqrt{x^3} - \sqrt{2y})(\sqrt{x^3} + \sqrt{2y})$
$(\sqrt{5x^5} + \sqrt{2})(\sqrt{5x^5} - \sqrt{2})$
$(\sqrt{a} + \sqrt{b})^2$
$(3 - \sqrt{2})^2$
$(\sqrt{8} + \sqrt{3})^2$
$(\sqrt{5} - \sqrt{b})^2$
$(2\sqrt{a} - 3\sqrt{b})^2$
$(3\sqrt{x} + 2\sqrt{y})^2$
PDF zum Drucken
Lösungs-PDF
Weitere Arbeitsblätter
Studienkolleg Vektoren, SS 2017
127 min, 10 Aufgaben #1818Übungsblatt der Hochschule Kaiserslautern, University of Applied Sciences, zum Thema Vektoren.
Ableitungsfunktion und ihre Anwendung
92 min, 12 Aufgaben #1590Aus einer Funktion macht man eine andere Funktion, die sogenannte Ableitungsfunktion. Die Aufgaben beschäftigen sich damit, wie das gemacht wird, und was man darüber hinaus mit der Ableitungsfunktion machen kann. Zum Beispiel Steigungswinkel, Schnittwinkel, Tangentengleichungen oder Berührpunkte bestimmen.
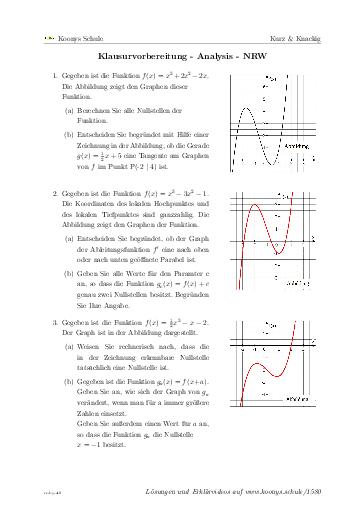
Klausurvorbereitung - Analysis - NRW
15 min, 3 Aufgaben #1580Drei kleine verschiedene Aufgaben zur Differentialrechnung. Man muss Sachen berechnen und begründete Entscheidungen geben. Dafür werden Potenzfunktionen 3. Grades mit Nullstellen, Tangenten, Ableitungen und Verschiebungen von Funktionen benutzt.
Textaufgaben mit mehreren Unbekannten
46 min, 11 Aufgaben #1336Elf Textaufgaben bei denen immer zunächst zwei Gleichungen mit zwei Unbekannten aufgestellt und dann gelöst werden müssen.
Bernoulli-Ketten Anwendung
37 min, 4 Aufgaben #1701Anwendungsaufgaben zu Bernoulli-Ketten. Die ersten zwei Aufgaben fragen die grundlegenden Berechnungen ab. Die dritte ist vom Typ mindestens-mindestens und die vierte zeichnet sich durch eine äußert schwierige Aufgabenstellung aus. Ein kühler Kopf ist hier gefragt.