Mathematische Kompetenzen - Zufall

Argumentieren

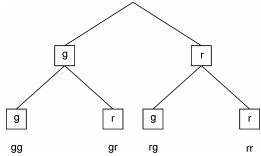
Eine Kiste enthält gut gemischt fünfzehn gelbe und zehn rote Bausteine. Zweimal nacheinander wird jeweils ein Baustein zufällig entnommen und wieder zurückgelegt. Simon soll die Wahrscheinlichkeit dafür bestimmen, dass die beiden entnommenen Bausteine unterschiedliche Farben haben.

Er zeichnet das abgebildete Baumdiagramm und folgert: Das Zufallsexperiment hat vier mögliche Ergebnisse, zwei davon erfüllen die gewünschte Bedingung.
Also gilt: $ \mathrm{P(\{gr;rg\})} = \frac{2}{4} = 50% $.

Begründe, dass Simons Überlegung falsch ist.

Probleme lösen

Eine Kiste enthält gut gemischt fünfzehn gelbe und zehn rote Bausteine. Zweimal nacheinander wird jeweils ein Baustein zufällig entnommen. Berechne auf der Grundlage zweier unterschiedlicher Annahmen jeweils die Wahrscheinlichkeit dafür, dass mindestens einer der entnommenen Bausteine rot ist.

Modellieren

Eine Kiste enthält gut gemischt fünfzehn gelbe und zehn rote Bausteine. Zweimal nacheinander wird jeweils ein Baustein zufällig entnommen. Charlotte und Marie stellen aufgrund dieser Informationen die Situation jeweils mit einem Baumdiagramm dar.

Erläutere, von welcher Voraussetzung Charlotte und Marie jeweils ausgegangen sind.

Darstellungen verwenden

Eine Kiste enthält gut gemischt fünfzehn gelbe und zehn rote Bausteine. Zweimal nacheinander wird jeweils ein Baustein zufällig entnommen und nicht wieder zurückgelegt. Jakob berechnet die Wahrscheinlichkeit dafür, dass die beiden entnommenen Bausteine unterschiedliche Farben haben:
$$ \frac{3}{5}\cdot\frac{5}{12} + \frac{2}{5}\cdot\frac{5}{8}=2\cdot\frac{1}{4}=50%.$$
Zeichne das zugehörige Baumdiagramm und trage alle in der Rechnung vorkommenden Brüche an der jeweils passenden Stelle ein.

Mit symbolischen, formalen und technischen Elementen der Mathematik umgehen

Eine Kiste enthält gut gemischt 25 Bausteine, von denen $ k\,(1\le k\le 24) $ gelb und die übrigen rot sind. Zweimal nacheinander wird jeweils ein Baustein zufällig entnommen und nicht wieder zurückgelegt. Die Wahrscheinlichkeit dafür, dass die beiden entnommenen Bausteine unterschiedliche Farben haben, wird durch den Term $ p(k) = 2\cdot \frac{k}{25}\cdot\frac{25-k}{24} $ angegeben. Bestimme $ k $ durch Rechnung so, dass $ p(k) = \frac{1}{3} $ gilt.

Kommunizieren

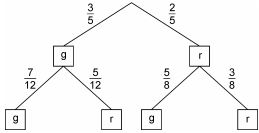
Eine Kiste enthält gut gemischt fünfzehn gelbe und zehn rote Bausteine. Zweimal nacheinander wird jeweils ein Baustein zufällig entnommen und nicht wieder zurückgelegt.

Hannah stellt die Situation durch das abgebildete Baumdiagramm dar. Beschreibe mit Worten, welche Bedeutung die angegebene Wahrscheinlichkeit $ \frac{3}{8} $ hat.