Einleitung
Klassenarbeit einer 8. Klasse auf einem Berliner Gymnasium.
Es müssen Terme vereinfacht und Gleichungen gelöst werden. Dabei müssen Klammern aufgelöst, binomische Formeln angewendet und Gleichungen aus Texten aufgestellt werden.
27 Minuten Erklärungen in 4 Aufgaben von Koonys Schule.
Aufgaben
Löse die Klammern auf und fasse so weit wie möglich zusammen.
$ -(-4x^2 - 3y + 5a) + (1,6a - x^2) - (0,2y + a) $
$ y(y-1) + 3(2y-1+y^2) - (-4 + 5y^2) $
$ 5ax\cdot 4b^2x\cdot (3a) $
$ (-2z)\cdot (3x)^2 \cdot az $
Löse die Gleichungen.
$ -17x-(27-15-8-5x) = -3x-37 + (67 + x) $
$ 2(9x-13) = 6(-4+2x) - 2 $
$ (8-x)^2 = (x+3)^2 $
$ (x+3)^2 - x(x+7) = (x-10)(x+10) + x(2-x) $
Ermittle die gesuchte Zahl, indem Du eine Gleichung aufstellt und löst.
Addiert man zur gesuchten Zahl 6,3, erhält man das Achtfache der gesuchten Zahl, vermindert um 2,1.
Wenn man von der gesuchten Zahl 7 subtrahiert, das Ergebnis vervierfacht und anschließend 42 addiert, erhält man 4.
PDF zum Drucken
Lösungs-PDF
Weitere Arbeitsblätter
Lernkontrolle Wahrscheinlichkeitsrechnung
36 min, 4 Aufgaben #7392Typische Aufgaben der Wahrscheinlichkeitsrechnung für die Sekundarstufe. Mit dabei sind Ergebnismengen, Baumdiagramme und Gewinnerwartung. Natürlich auch Urnen, viele Kugeln und Lotterielose.
Kreise - Anwendung
59 min, 5 Aufgaben #8890In verschiedenen Anwendungsaufgaben müssen die Kreisformeln genutzt werden. Umstellen der Formeln, Kreisausschnitte, Prozent- und Geschwindigkeitsrechnung müssen darüber hinaus angewendet werden.
Übungen zu kombinatorischen Abzählverfahren
29 min, 8 Aufgaben #1648Ob mit oder ohne Reihenfolge und mit oder ohne Wiederholung: die Frage, die sich stellt, ist immer die gleiche: wie viele Möglichkeiten gibt es? Bei den Aufgaben kommt man noch häufig durch Abzählen zur Lösung.
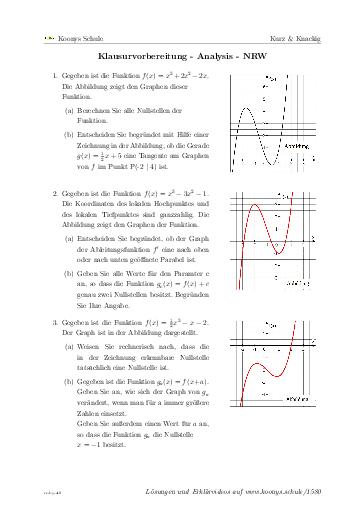
Klausurvorbereitung - Analysis - NRW
15 min, 3 Aufgaben #1580Drei kleine verschiedene Aufgaben zur Differentialrechnung. Man muss Sachen berechnen und begründete Entscheidungen geben. Dafür werden Potenzfunktionen 3. Grades mit Nullstellen, Tangenten, Ableitungen und Verschiebungen von Funktionen benutzt.
Ikarus Abitur GK Berlin 2016
64 min, 6 Aufgaben #1980Abituraufgabe zur analytischen Geometrie für den Grundkurs mit 30 erreichbaren Bewertungseinheiten aus Berlin 2016.