Einleitung
Eine Einführung in quadratische Funktionen.
Begonnen wird mit der Normalparabel. Das wird weiter und weiter ausgebaut bis hin zur Scheitelpunktsform und beendet mit der Übung diese in die allgemeine Form zu überführen.
Ausblick könnte die quadratische Ergänzung sein.
53 Minuten Erklärungen in 6 Aufgaben von Koonys Schule.
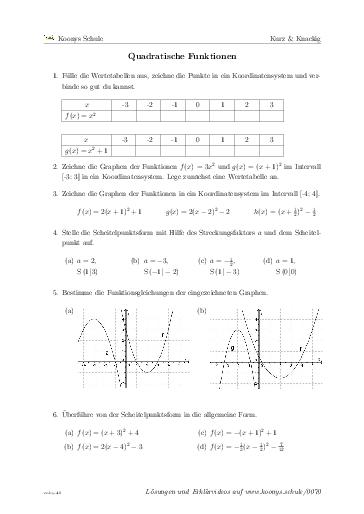
Aufgaben
Fülle die Wertetabellen aus, zeichne die Punkte in ein Koordinatensystem und verbinde so gut du kannst.
| $x$ | -3 | -2 | -1 | 0 | 1 | 2 | 3 |
| $ f(x)=x^2 $ |
| $x$ | -3 | -2 | -1 | 0 | 1 | 2 | 3 |
| $ g(x)=x^2+1 $ |
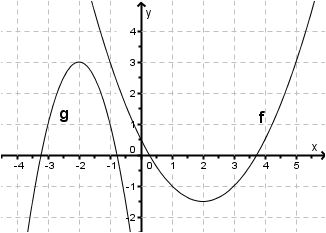
Zeichne die Graphen der Funktionen $ f(x) = 3x^2 $ und $ g(x) = (x+1)^2 $ im Intervall [-3; 3] in ein Koordinatensystem. Lege zunächst eine Wertetabelle an.
Zeichne die Graphen der Funktionen in ein Koordinatensystem im Intervall [-4; 4].
$ f(x)=2(x+1)^2 + 1 $
$ g(x) = 2(x-2)^2 - 2 $
$ h(x) = (x+\frac{1}{2})^2 - \frac{1}{2} $
Stelle die Scheitelpunktsform mit Hilfe des Streckungsfaktors $ a $ und dem Scheitelpunkt auf.
$ a = 2 $,
$ \EPUNKT{S}{1}{3} $
$ a = -3 $,
$ \EPUNKT{S}{-1}{-2} $
$ a = -\frac{1}{2} $,
$ \EPUNKT{S}{1}{-3} $
$ a = 1 $,
$ \EPUNKT{S}{0}{0} $
Überführe von der Scheitelpunktsform in die allgemeine Form.
$ f(x) = (x+3)^2 + 4 $
$ f(x) = 2(x-4)^2 - 3 $
$ f(x) = -(x+1)^2 + 1 $
$ f(x) = -\frac{1}{3}(x-\frac{1}{2})^2 - \frac{7}{12}$
Weitere Arbeitsblätter
Einführung Terme
65 min, 8 Aufgaben #2826Erste Aufgaben zu Termen. Termwerte berechen, Terme vergleichen und Textgleichungen in beide Richtungen: sowohl Gleichungen aus Texten aufstellen aber auch Texte basierend auf Gleichungen verfassen. Die Hälfte der Aufgaben beschäftigt sich mit dem Zusammenfassen von Termen.
Ableitungsfunktion und ihre Anwendung
92 min, 12 Aufgaben #1590Aus einer Funktion macht man eine andere Funktion, die sogenannte Ableitungsfunktion. Die Aufgaben beschäftigen sich damit, wie das gemacht wird, und was man darüber hinaus mit der Ableitungsfunktion machen kann. Zum Beispiel Steigungswinkel, Schnittwinkel, Tangentengleichungen oder Berührpunkte bestimmen.
kgV und ggT
50 min, 6 Aufgaben #0010Primfaktorzerlegung, größter gemeinsamer Teiler und kleinstes gemeinsames Vielfaches nimmt die Hälfte des Blattes ein. Die andere Hälfte sind Anwendungsaufgaben.
BBR - Vergleichsarbeit Mathematik
59 min, 14 Aufgaben #2508Die Vergleichende Arbeit 2015 im Fach Mathematik zum Erwerb der Berufsbildungsreife bzw. des Hauptschulabschlusses. Bearbeitungszeit: 90 Minuten. Zugelassene Hilfsmittel: Formelübersicht und wissenschaftlicher nicht grafikfähiger Standard-Taschenrechner.
Gleichungen in Texten
54 min, 11 Aufgaben #1337Zwei Gleichungen aufstellen und dann lösen. Immer. Zum Teil sehr knifflig!