Einleitung
Das Vereinfachen von Termen mit Klammern wird Stück für Stück gezeigt.
Mit dabei sind Minusklammern, das einfache und das doppelte Distributivgesetz.
Nach den Aufgaben ist man fachlich soweit sich als nächstes an die binomischen Formeln vagen zu können.
35 Minuten Erklärungen in 8 Aufgaben von Koonys Schule.
Aufgaben
Löse die Klammer auf.
$-(4+a)$
$-(b-3)$
$-(-a+7)$
$-(a+b)$
$-(x-y)$
$-(-2c-4d)$
$-(8a^2-13b^2)$
$-(-4c-5d-7e)$
$-(17x-9y-12z)$
$x-(y+z)$
$a-(b-c)$
$x-(-7+y)$
$4a-(a-b)$
$6r-(5s-8r)$
$9x-(4y+5x)$
$23c-(-9d+8c)$
$12-(4-x+y)$
$29c-(-7d-3c-5e)$
Löse die Klammern auf und fasse zusammen.
$3(x+2y)-3x$
$x(3+2x) + 2(x^2-x)$
$-3(a+b)-4a$
$-4(2a-5b) - 8b$
$3b-3(b-a)$
$5(x+3y) - 5x$
$(a+b)(a^2 - ab + b^2)$
$(a-b)(a^2-ab+b^2)$
$(2a+3b)(5a-6b+1)$
$(3x + 2y)(9x-2y-3z)$
$(5a-6b+3c)(7a-5c)$
$(10u-5v+8)(20u-13v)$
Weitere Arbeitsblätter
Klammern auflösen
51 min, 5 Aufgaben #3335Aufgaben zum Vereinfachen von Termen mit Klammern. Zunächst Terme mit Minusklammern, dann welche mit doppelten Klammern (doppeltes Distributivgesetz). Am Ende, so ganz nebenbei, die binomischen Formeln und der ganze Spaß rückwärts: das Ausklammern.
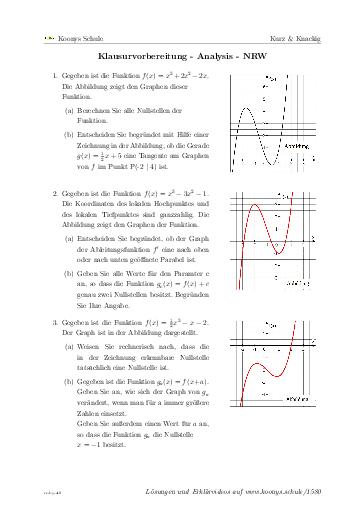
Klausurvorbereitung - Analysis - NRW
15 min, 3 Aufgaben #1580Drei kleine verschiedene Aufgaben zur Differentialrechnung. Man muss Sachen berechnen und begründete Entscheidungen geben. Dafür werden Potenzfunktionen 3. Grades mit Nullstellen, Tangenten, Ableitungen und Verschiebungen von Funktionen benutzt.
Kathetensatz und Höhensatz
37 min, 6 Aufgaben #0045Eine Hälfte beschäftigt sich mit Berechnungen am rechtwinkligen Dreieck. Die andere Hälfte sind schwierigere Textaufgaben.
Vermischte Übungen MSA
36 min, 6 Aufgaben #1290Textgleichungen, Gleichungen mit vielen Klammern, Gleichungssysteme, Textaufgaben zu Körperberechnungen und Wahrscheinlichkeiten sind Inhalt dieses Arbeitsblattes. Anspruchsvolle Aufgaben quer durchs Beet.
Stammfunktionen und Flächeninhalte
76 min, 8 Aufgaben #8010Wie für das Thema üblich werden zunächst einfache Polynomfunktionen integriert und dann schwierigere Funktionen bei denen zunächst Potenz- und Wurzelgesetze angewendet werden müssen. Der Aufgabentyp mit gegebener Ableitung und einem Punkt die Ausgangsfunktion zu bestimmen ist auch dabei und die zweite Hälfte der Aufgaben behandelt die Flächenberechnung zwischen Graph und x-Achse. Dabei müssen zuerst die Nullstellen bestimmt werden. :)