Einleitung
Drei kleine verschiedene Aufgaben zur Differentialrechnung. Man muss Sachen berechnen und begründete Entscheidungen geben.
Dafür werden Potenzfunktionen 3. Grades mit Nullstellen, Tangenten, Ableitungen und Verschiebungen von Funktionen benutzt.
15 Minuten Erklärungen in 3 Aufgaben von Koonys Schule.
Aufgaben
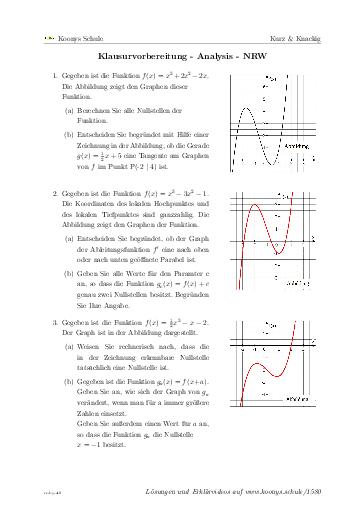
Gegeben ist die Funktion $f(x) = x^3+2x^2-2x$. Die Abbildung zeigt den Graphen dieser
Funktion.
Berechnen Sie alle Nullstellen der
Funktion.
Entscheiden Sie begründet mit Hilfe einer Zeichnung in der Abbildung, ob die Gerade $g(x) = \frac{1}{2}x+5$ eine Tangente am Graphen von $f$ im Punkt P(-2 $\vert$ 4) ist.
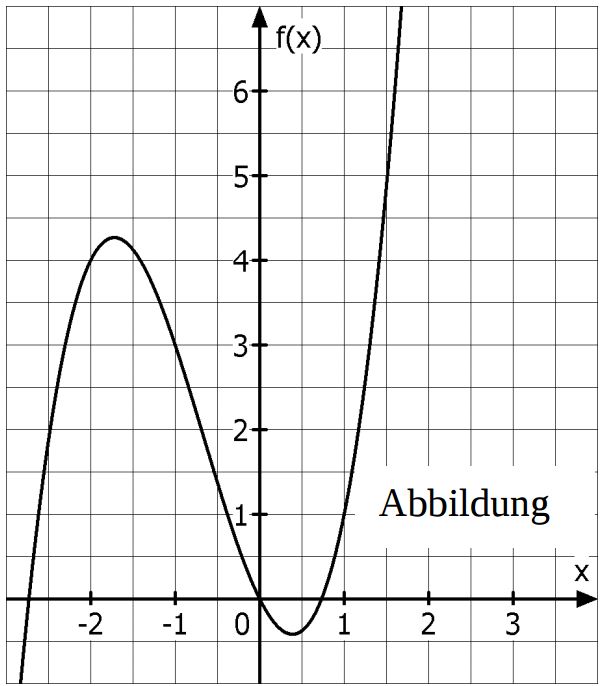
Gegeben ist die Funktion $f(x) = x^3-3x^2-1$. Die Koordinaten des lokalen Hochpunktes und des lokalen Tiefpunktes sind ganzzahlig. Die Abbildung zeigt den Graphen der Funktion.
Entscheiden Sie begründet, ob der Graph der Ableitungsfunktion $f'$ eine nach oben oder nach unten geöffnete Parabel ist.
Geben Sie alle Werte für den Paramter c an, so dass die Funktion $g_c(x) = f(x) + c$ genau zwei Nullstellen besitzt. Begründen Sie Ihre Angabe.
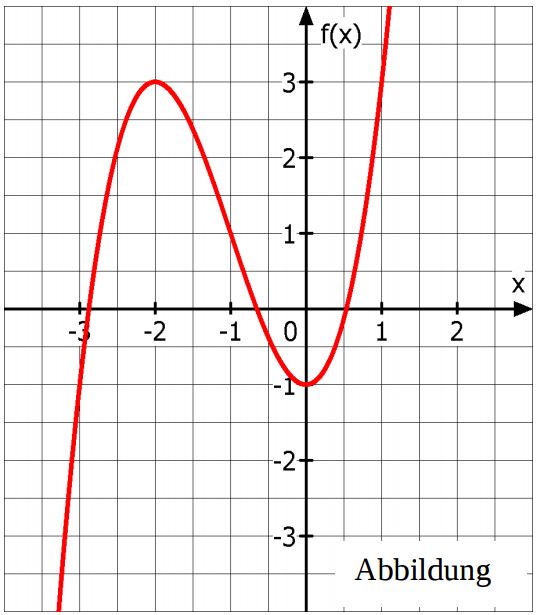
Gegeben ist die Funktion $f(x) = \frac{1}{2}x^3 - x- 2$. Der Graph ist in der Abbildung dargestellt.
Weisen Sie rechnerisch nach, dass die in der Zeichnung erkennbare Nullstelle tatsächlich eine Nullstelle ist.
Gegeben ist die Funktion $g_a(x) = f(x+a)$. Geben Sie an, wie sich der Graph von $g_a$ verändert, wenn man für a immer größere Zahlen einsetzt.
Geben Sie außerdem einen Wert für $ a $ an, so dass die Funktion $g_a$ die Nullstelle
$x=-1$ besitzt.
Weitere Arbeitsblätter
Ebenengleichungen
22 min, 4 Aufgaben #1925Überblick aller drei Arten von Ebenengleichungen und wie man jeweils von einer Form in die andere kommt. Paramatergleichung, Normalengleichung und Koordinantengleichungen werden alle untereinander umgeformt.
Klammern auflösen
56 min, 9 Aufgaben #3337Alle Möglichkeiten von Klammern auf einem Blatt. Mit diesen Übungen kann beim Auflösen von Klammern gar nichts mehr schief laufen.
Klassenarbeit - Wurzelgesetze und Potenzgesetze
24 min, 6 Aufgaben #0995Originale Arbeit mit 36 erreichbaren Punkten.
Arbeit - ganzrationale Funktionen
49 min, 3 Aufgaben #1520Klassenarbeit über ganzrationale Funktionen mit 55 erreichbaren Punkten.
Weidezelt Abitur GK Berlin 2016
64 min, 6 Aufgaben #1611Abituraufgabe zur Analysis für den Grundkurs mit 40 erreichbaren Bewertungseinheiten aus Berlin 2016. Neben Nullstellen, Extrempunkten und Wendepunkten sind außerdem dabei: Extremalproblem, Rekonstruktion einer quadratischen Funktion und Flächenberechnung.