Einleitung
Aufgaben zum Vereinfachen von Termen mit Klammern. Zunächst Terme mit Minusklammern, dann welche mit doppelten Klammern (doppeltes Distributivgesetz).
Am Ende, so ganz nebenbei, die binomischen Formeln und der ganze Spaß rückwärts: das Ausklammern.
51 Minuten Erklärungen in 5 Aufgaben von Koonys Schule.
Aufgaben
Löse erst die Klammern auf und fasse dann zusammen.
$(x-y)-(x+y)$
$(r+s)-(r-s)$
$4a-(a-b)$
$(5-x)-(x-7)$
$-(4x-7)-(10-3)$
$(21a+13b)-(-5a+7b)$
$75x-(18x-9y)-(3y-4x)$
$45a+(41a+39b)-(8b+52a)$
Löse die Klammern auf.
$(a+b)(c-d)$
$(a-b)(c-d)$
$(a+3)(b+8)$
$(y-7)(4-z)$
$(3a-2)(4b+8)$
$(4x-5)(7z+7)$
$(2a-10)(-b-13)$
$(5a+3b)(4c+7d)$
$(5r-2s)(3u+4v)$
Löse erst die Klammern auf und fasse dann zusammen.
$(a-4)(a+5)$
$(z+7)(z-6)$
$(10-b)(7+b)$
$(1-x)(x-1)$
$(a + 3b)(a+b)$
$(3x+2y)(x+4y)$
$(7a-3b)(4a-6b)$
$(-x-2y)(-x+y)$
$(3y+7z)(5z+4y)$
Löse erst die Klammern auf und fasse dann zusammen.
$(x+y)^2$
$(x-y)^2$
$(x+y)(x-y)$
$(b+7)^2$
$(u-2)^2$
$(z-\frac{1}{2})^2$
$(3a+b)^2$
$(\frac{1}{2}r - \frac{3}{4})^2$
$(9-2z)(9+2z)$
Klammere aus.
$5x + 5y$
$5xy - 6xz$
$7xy + 7xz$
$0,5a^2b - 3ab^2$
$ax + bx + cx$
$15a^2 - 25ab$
$24xy^2 + 18yz^2$
$12a^3bx^2-30abx-6ab^2x^2$
Weitere Arbeitsblätter
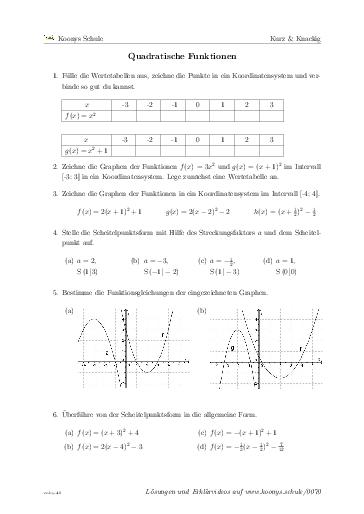
Quadratische Funktionen
53 min, 6 Aufgaben #0070Eine Einführung in quadratische Funktionen. Begonnen wird mit der Normalparabel. Das wird weiter und weiter ausgebaut bis hin zur Scheitelpunktsform und beendet mit der Übung diese in die allgemeine Form zu überführen. Ausblick könnte die quadratische Ergänzung sein.
Glücksrad mit Urne - Übungsaufgabe Stochastik LK
21 min, 6 Aufgaben #1710Eine Übungsaufgabe, die Urne und Glücksrad kombiniert. Nebst Baumdiagrammen, Bernoulli und der summierten Binomialverteilung werden auch Gewinnerwartung und Prozentrechnung beim Kreis benötigt.
Textaufgaben mit mehreren Unbekannten
46 min, 11 Aufgaben #1336Elf Textaufgaben bei denen immer zunächst zwei Gleichungen mit zwei Unbekannten aufgestellt und dann gelöst werden müssen.
Abzählverfahren
35 min, 6 Aufgaben #1651Verschiedene Aufgaben mit Würfel-Würfen und Zahlen mit ihren Ziffern. Gefragt ist jedes mal nach der Wahrscheinlichkeit, dass ein bestimmtes Ereignis passiert. Schwierigkeit liegt darin herauszufinden, was die Anzahl aller Ergebnisse und die Anzahl der günstigen Ergebnisse ist.
Kleine vermischte Übungen - Klasse 8
50 min, 12 Aufgaben #5200Bunt gemischte Textaufgaben zu verschiedenen Themen der 8. Klasse und darüber hinaus. Etwas zum Knobeln für Schüler am Anfang des Schuljahres.