Einleitung
Das kleine Einmaleins wird hier sehr wichtig: Brüche kürzen und erweitern. Dazu stellt dieses Arbeitsblatt Aufgaben zur Verfügung.
64 Minuten Erklärungen in 6 Aufgaben von Koonys Schule.
Aufgaben
Kürze so weit wie möglich.
$\frac{2}{4}$ ; $\frac{6}{8}$ ; $\frac{4}{10}$ ; $\frac{4}{12}$ ; $\frac{7}{14}$ ; $\frac{10}{16}$ ; $\frac{8}{20}$ ; $\frac{9}{14}$
$\frac{4}{6}$ ; $\frac{9}{12}$ ; $\frac{3}{9}$ ; $\frac{8}{18}$ ; $\frac{21}{27}$ ; $\frac{15}{27}$ ; $\frac{20}{35}$ ; $\frac{21}{35}$
$\frac{12}{14}$ ; $\frac{12}{15}$ ; $\frac{12}{16}$ ; $\frac{12}{18}$ ; $\frac{12}{20}$ ; $\frac{12}{21}$ ; $\frac{12}{24}$ ; $\frac{12}{26}$
$\frac{30}{32}$ ; $\frac{18}{32}$ ; $\frac{17}{34}$ ; $\frac{15}{35}$ ; $\frac{2}{36}$ ; $\frac{6}{36}$ ; $\frac{14}{36}$ ; $\frac{21}{36}$
$\frac{10}{4}$ ; $\frac{30}{8}$ ; $\frac{15}{6}$ ; $\frac{18}{6}$ ; $\frac{30}{12}$ ; $\frac{40}{12}$ ; $\frac{50}{12}$ ; $\frac{40}{15}$
$\frac{27}{45}$ ; $\frac{45}{30}$ ; $\frac{64}{32}$ ; $\frac{52}{65}$ ; $\frac{72}{18}$ ; $\frac{72}{24}$ ; $\frac{75}{30}$ ; $\frac{60}{15}$
Erweitere $\frac{1}{2}$, $\frac{2}{3}$, $\frac{3}{5}$, $\frac{5}{8}$, $\frac{4}{9}$, $\frac{10}{3}$, $\frac{11}{8}$, $\frac{12}{5}$ mit
Kürze so weit wie möglich.
Bestimme den fehlenden Zähler x.
Ergänze den fehlenden Nenner x.
Mache gleichnamig.
$\frac{2}{3}$ ; $\frac{7}{12}$
$\frac{3}{5}$ ; $\frac{8}{15}$
$\frac{3}{4}$ ; $\frac{5}{6}$
$\frac{3}{4}$ ; $\frac{1}{6}$
$\frac{2}{3}$ ; $\frac{11}{18}$
$\frac{3}{4}$ ; $\frac{4}{5}$
$\frac{2}{7}$ ; $\frac{1}{2}$
$\frac{3}{8}$ ; $\frac{7}{10}$
$\frac{3}{4}$ ; $\frac{11}{12}$
$\frac{2}{3}$ ; $\frac{3}{4}$
$\frac{5}{6}$ ; $\frac{3}{8}$
$\frac{3}{10}$ ; $\frac{5}{12}$
Alle Erklärungen sind auch in einer
PDF zum Drucken
Lösungs-PDF
Weitere Arbeitsblätter
Terme vereinfachen
35 min, 4 Aufgaben #2832Übungen zum Vereinfachen von Termen durch die vier Grundrechenarten: Addition, Subtraktion, Multiplikation und Division. Unter anderem müssen gleichartige Glieder zusammengefasst und Klammern aufgelöst werden.
Klassenarbeit - Rechnen mit Wurzeln
27 min, 9 Aufgaben #0993Originale Arbeit einer 9. Klasse mit 60 möglichen Punkten ohne Taschenrechner zur Wurzelrechnung.
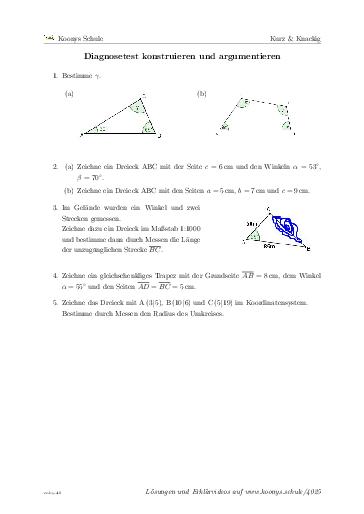
Diagnosetest konstruieren und argumentieren
36 min, 5 Aufgaben #4025Aufgaben zur Konstruktion von Dreiecken mit Hilfe der Kongruenzsätze. Außerdem kommen Innenwinkelsatz, ein gleichschenkliges Trapez und die Konstruktion des Umkreises eines Dreiecks im Koordinatensystem vor.
Prozentrechnung - Grundlagen
81 min, 5 Aufgaben #0100Hier geht es um pures Rechnen. Zunächst wird der Zusammenhang von Prozenten und Brüchen geübt und im Anschluss die drei grundlegenden Aufgabentypen der Prozentrechnung.
Klassenarbeit binomische Formeln
33 min, 8 Aufgaben #3132Klassenarbeit einer 8. Klasse in Berlin aus dem Jahre 2015.