Einleitung
Der Differenzenquotient muss gebildet und Funktionen abgeleitet werden. Darüber hinaus muss eine Ausgangsfunktion gezeichnet und Funktionsgleichungen von Ausgangsfunktionen gebildet werden.
Eine Aufgabe über die Differenzierbarkeit einer Betragsfunktion an einer bestimmten Stelle ist auch dabei.
34 Minuten Erklärungen in 8 Aufgaben von Koonys Schule.
Aufgaben
Zeigen Sie, dass die Funktion $ f $ mit $ f(x) = x^2 + 2 $ an jeder Stelle ihres Definitionsbereichs differenzierbar ist.
Hinweis: Bilden Sie den Differenzenquotienten an einer beliebigen Stelle $ x_0 $ und bestimmen Sie $ f'(x_0) $.
Bestimmen Sie die Ableitungsfunktion mithilfe der Ableitungsregeln:
$ f(x) = 5x^7 $
$ f(x) = 4x^3 - 3x^2 $
$ f(x) = 0,5x^5 - 2x^3 $
$ f(x) = x^5 + \frac{1}{4}x^4 + \frac{1}{2} x^3 - x $
$ f(x) = ax^2 + bx + c $
$ f(x) = 3x^{20} - 2x^2 $
$ f(x) = \frac{1}{5}(x^2 + x + 5) $
$ f(x) = 2x^2(3x+4) $
Bestimmen Sie die Stellen $ x_i $ an denen die Graphen der Funktionen $ f $ und $ g $ mit $ f(x) = 0,5x^2 - x^3 + 2 $ und $ g(x) = x^3 - 4 $ den gleichen Anstieg haben.
Leiten Sie aus dem dargestellten Graphen der Ableitungsfunktion $ f' $ Aussagen über das Steigungsverhalten der Funktion $ f $ ab.
Welches Verhalten zeigt $ f $ an der Stelle $ x = -2 $?
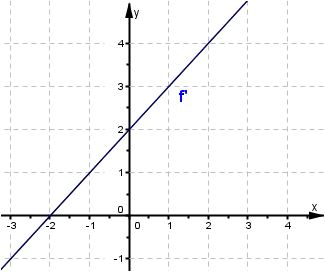
Bestimmen Sie zu den folgenden Ableitungen von Potenzfunktionen jeweils eine zugehörige Ausgangsfunktion:
$ f'(x) = 4x^3 $
$ f'(x) = 8x^7$
$ f'(x) = 0$
$ f'(t) = 10t^4$
Zeigen Sie, dass die Funktion $ f $ mit $ f(x) = |x|\cdot(1-x) $ an der Stelle $ x = 0 $ nicht differenzierbar ist.
Alle Erklärungen sind auch in einer
PDF zum Drucken
Lösungs-PDF
Weitere Arbeitsblätter
Smartphones Abitur GK Berlin 2016
44 min, 6 Aufgaben #1991Abituraufgabe zur analytischen Geometrie für den Grundkurs mit 30 erreichbaren Bewertungseinheiten aus Berlin 2016.
Terme addieren und subtrahieren
43 min, 8 Aufgaben #2828Terme vereinfachen indem man gleichartige Glieder zusammenfasst und ggf. vorher noch ein paar Klammern auflöst. Auch müssen Terme aufgestellt und Zahlenmauern gelöst werden.
Extremwertaufgaben
80 min, 8 Aufgaben #1597Acht verschiedene Aufgaben mit immer derselben Fragen: wann wird's maximal bzw. minimal? Sei es mit einem Schiff, in einer Spielzeugfabrik, auf einer Wiese oder als Motorradfahrer: überall muss zuerst eine Hauptbedingung und eine Nebenbedingung aufgestellt und dann zusammen in eine Funktion gepackt werden. Letztlich wird von dieser dann jedes mal der Extrempunkt bestimmt.
Wochenübung mit Klammern und Gleichungen
29 min, 7 Aufgaben #12347 Aufgaben für 7 Tage. Es müssen Klammern aufgelöst, Terme zusammengefasst und vor allem Gleichungen gelöst werden. Dabei treten unter anderem auch mal Brüche, die binomischen Formeln und die pq-Formel mit auf.
Sinus - Kosinus - Tangens
41 min, 6 Aufgaben #7000Sinus, Kosinus und Tangens von leicht bis schwer. Zunächst Aufgaben mit den Gleichungen und all ihren Varianten. Danach Standard-Aufgaben an rechtwinkligen Dreiecken und die zweite Hälfte sind Textaufgaben bei denen das gleiche noch einmal drankommt mit dem gewissen Etwas, das anspruchsvolle Aufgaben ausmacht.






