Einleitung
Textaufgaben über Stoffe, die exponentiell Zerfallen. Wertetabellen, Prozente und Halbwertszeiten kommen unter anderem vor.
Es sind im Wesentlichen verschiedene Aufgaben zu Exponentialfunktionen deren Wachstumsfaktor kleiner als 1 ist.
58 Minuten Erklärungen in 5 Aufgaben von Koonys Schule.
Aufgaben
Von einem radioaktiven Stoff sind 60,0s nach Beginn der Messung 54,2 % der vorhandenen Kerne zerfallen.
Nach welcher Zeit beträgt die Anzahl der vorhandenen Kerne nur noch 15,0 % der Ausgangsmenge?
Ein radioaktives Präparat zerfällt so, dass die vorhandene Substanz nach jeweils 7 Tagen auf ein Fünftel zurückgeht. Zu Beginn der Beobachtung sind 15mg der Substanz vorhanden.
Bestimme die Exponentialgleichung, die diesem Zerfall zugrunde liegt.
Nach wie viel Tagen ist noch 1mg der ursprünglichen Substanz vorhanden?
Bestimme die Halbwertszeit des Präparats.
Bei Schilddrüsenerkrankungen bekommt der Patient radioaktives Jod gespritzt. Weil die Schilddrüse die einzige Stelle im Körper ist, die Jod braucht, landet all dieses radioaktive Jod dort. Radioaktives Jod besitzt eine Halbwertszeit von ungefähr 8 Tagen.
Nach wie vielen Tagen sind weniger als 2 Promille der Anfangsdosis vorhanden?
Der radioaktive Stoff Radium besitzt eine Halbwertszeit von 1590 Jahren.
Bestimme die Funktionsgleichung in der Form $ y = y_o \cdot 10^{kt} $.
Nach welcher Zeit sind noch 75 % der ursprünglichen Masse vorhanden?
Die Masse einer radioaktiven Substanz wird minütlich ermittelt. Man erhält folgende Tabelle:
| 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| 75 | 71.6 | 68.4 | 65.3 | 62.3 | 59.5 | 56.8 |
Prüfe, ob es sich um exponentiellen Zerfall handelt.
Ermittle das Zerfallsgesetz und die Halbwertszeit.
Nach welcher Zeit ist noch 1 % der ursprünglichen Masse vorhanden?
Weitere Arbeitsblätter
Klassenarbeit - Wurzelgesetze und Potenzgesetze
24 min, 6 Aufgaben #0995Originale Arbeit mit 36 erreichbaren Punkten.
Wurzelterme vereinfachen ohne Taschenrechner
41 min, 13 Aufgaben #0990Viele verschiedene Aufgaben zum Zusammenfassen von Wurzeltermen. Dabei werden neben den Wurzelgesetzen auch binomische Formeln benötigt.
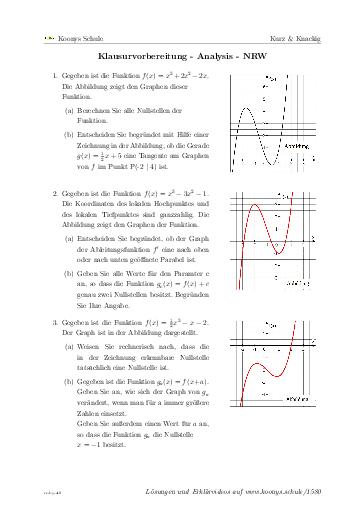
Klausurvorbereitung - Analysis - NRW
15 min, 3 Aufgaben #1580Drei kleine verschiedene Aufgaben zur Differentialrechnung. Man muss Sachen berechnen und begründete Entscheidungen geben. Dafür werden Potenzfunktionen 3. Grades mit Nullstellen, Tangenten, Ableitungen und Verschiebungen von Funktionen benutzt.
Einführung Terme
65 min, 8 Aufgaben #2826Erste Aufgaben zu Termen. Termwerte berechen, Terme vergleichen und Textgleichungen in beide Richtungen: sowohl Gleichungen aus Texten aufstellen aber auch Texte basierend auf Gleichungen verfassen. Die Hälfte der Aufgaben beschäftigt sich mit dem Zusammenfassen von Termen.
Pythagoras - Anwendungen
49 min, 6 Aufgaben #0040Anwendungsaufgaben mit dem Satz des Pythagoras. Unter anderem werden Diagonale von Quadrat und Würfel berechnet, Berechnungen am gleichschenkligen Dreieck, Pyramide und Walmdach durchgeführt u.v.m.