Einleitung
7 Aufgaben für 7 Tage. Es müssen Klammern aufgelöst, Terme zusammengefasst und vor allem Gleichungen gelöst werden. Dabei treten unter anderem auch mal Brüche, die binomischen Formeln und die pq-Formel mit auf.
29 Minuten Erklärungen in 7 Aufgaben von Koonys Schule.
Aufgaben
Weitere Arbeitsblätter
BBR - Vergleichsarbeit Mathematik
59 min, 14 Aufgaben #2508Die Vergleichende Arbeit 2015 im Fach Mathematik zum Erwerb der Berufsbildungsreife bzw. des Hauptschulabschlusses. Bearbeitungszeit: 90 Minuten. Zugelassene Hilfsmittel: Formelübersicht und wissenschaftlicher nicht grafikfähiger Standard-Taschenrechner.
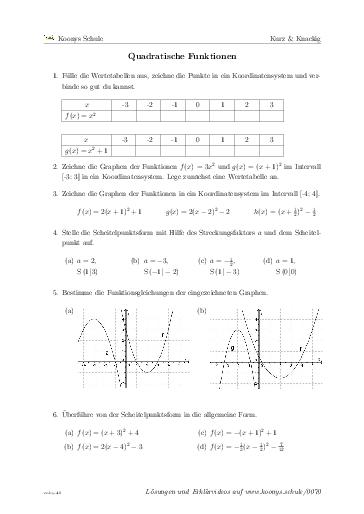
Quadratische Funktionen
53 min, 6 Aufgaben #0070Eine Einführung in quadratische Funktionen. Begonnen wird mit der Normalparabel. Das wird weiter und weiter ausgebaut bis hin zur Scheitelpunktsform und beendet mit der Übung diese in die allgemeine Form zu überführen. Ausblick könnte die quadratische Ergänzung sein.
Quadratische Gleichungen
40 min, 5 Aufgaben #0060Die Aufgaben führen schrittweise an das Lösen von reinquadratischen Gleichungen verschiedener Formen heran.
Strahlensätze *
27 min, 3 Aufgaben #4181Die Strahlensätze werden zunächst an klassischen Aufgaben mit gegebener Skizze gezeigt und im Anschluss an Textaufgaben gefestigt.
Ebenengleichungen
22 min, 4 Aufgaben #1925Überblick aller drei Arten von Ebenengleichungen und wie man jeweils von einer Form in die andere kommt. Paramatergleichung, Normalengleichung und Koordinantengleichungen werden alle untereinander umgeformt.