Einleitung
Klassenarbeit einer 8. Klasse in Berlin aus dem Jahre 2015.
33 Minuten Erklärungen in 8 Aufgaben von Koonys Schule.
Aufgaben
Lies dir alle Aufgaben gut durch und entscheide dann, mit welcher Aufgabe du beginnen willst.
Schreibe ordentlich und zeichne sauber mit Bleistift und Lineal.
Fülle die Lücken mit Hilfe der binomischen Formeln aus.
$ 9n^2 + 48mn + \text{__} = \left( \,\text{__} + 8m\right)^2 $
$ 169 - \text{__} = (\,\text{__} + \frac{1}{2})(\,\text{__} - \frac{1}{2}) $
$ z^2 - \,\text{__} + 144 = \left(\,\text{__} - 12\right)^2 $
Löse die Klammern auf und fasse, wenn möglich, zusammen.
$6\cdot (b-5)$
$ (-3a)\cdot(5a + 6b - 12) $
$ (x+5)(x+7) $
$ (6m+7n)(4m-n) $
Berichtige Maxs Ergebnisse auf der rechten Seite der Gleichung.
$ \left(4a+4\right)^2 = 16a^2 + 16a + 16 $
$\left(9x-8\right)^2 = 81x^2 - 126x + 64 $
$ 16y^2z^2 - 96xyz^2 + 144x^2z^2 = \left(4yz - 13xz\right)^2 $
Die Kinder Max und Angelika wollen ihre Zimmer tauschen. Angelikas altes Zimmer ist quadratisch. Maxs rechteckiges Zimmer ist im Vergleich zu dem quadratischen auf der einen Seite um $ 0,70\,\mathrm{m} $ verkürzt und auf der anderen Seite um $ 0,70\,\mathrm{m} $ verlängert. Sind die Zimmer gleich groß?
(Tipp: Stelle zuerst für jeden Flächeninhalt einen Term auf.)
Der Pausenhof des Bundestages soll neu gestaltet werden. Bisher ist eine quadratische Fläche $ x^2 $ mit Kies bedeckt. Die Rasenfläche erhält man, wenn man zur Kiesfläche an der einen Seite $ 2\,\mathrm{m} $ dazurechnet und an der anderen $ 4\,\mathrm{m} $ abzieht. Wie groß ist die Rasenfläche?
Zusatzaufgabe
Ein Bauer hat sein Kartoffelfeld vergrößert. Die neue Fläche beträgt: $ x^2 + 120x + 360 $. Um welche Länge (in m) hat der Bauer sein Feld auf jeder Seite erweitert?
Weitere Arbeitsblätter
Wochenübung mit Klammern und Gleichungen
29 min, 7 Aufgaben #12347 Aufgaben für 7 Tage. Es müssen Klammern aufgelöst, Terme zusammengefasst und vor allem Gleichungen gelöst werden. Dabei treten unter anderem auch mal Brüche, die binomischen Formeln und die pq-Formel mit auf.
Textgleichungen mit Brüchen für Profis 1v3
39 min, 8 Aufgaben #1341Textaufgaben müssen gelöst werden indem man Gleichungen aufstellt bei denen Brüche vorkommen.
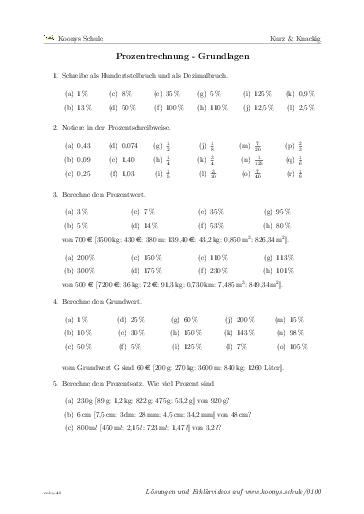
Prozentrechnung - Grundlagen
81 min, 5 Aufgaben #0100Hier geht es um pures Rechnen. Zunächst wird der Zusammenhang von Prozenten und Brüchen geübt und im Anschluss die drei grundlegenden Aufgabentypen der Prozentrechnung.
Test über Vorkenntnisse zu ganzrationalen Funktionen
31 min, 4 Aufgaben #1515Originaler Test mit 40 erreichbaren Punkten.
Extremwertaufgaben
72 min, 7 Aufgaben #1599Sieben verschiedene Aufgaben mit immer derselben Fragen: wann wird's maximal bzw. minimal? Sei es ein Rechteck im Kreis, der Graph einer Funktion, eine Konservendose oder eine Marmorplatte: überall muss zuerst eine Hauptbedingung und eine Nebenbedingung aufgestellt und dann zusammen in eine Funktion gepackt werden. Letztlich wird von dieser dann jedes mal der Extrempunkt bestimmt.