Einleitung
Die Vergleichende Arbeit 2015 im Fach Mathematik zum Erwerb der Berufsbildungsreife bzw. des Hauptschulabschlusses.
Bearbeitungszeit: 90 Minuten.
Zugelassene Hilfsmittel: Formelübersicht und wissenschaftlicher nicht grafikfähiger Standard-Taschenrechner.
59 Minuten Erklärungen in 14 Aufgaben von Koonys Schule.
Aufgaben
Max nimmt sich vor, jeden Tag Mathematik zu üben. Am ersten Tag übt er 10 Minuten. Am zweiten Tag übt er doppelt so lange wie am ersten, am dritten Tag doppelt so lange wie am zweiten Tag.
Wie lange übt er am dritten Tag?
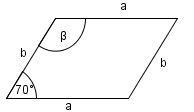
Was für ein Viereck ist abgebildet?
Wie groß ist der Winkel $ \beta $?
(Skizze nicht maßstabsgerecht.)
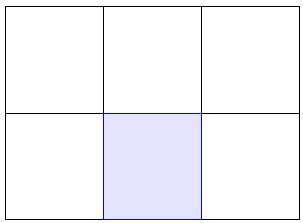
Das Rechteck besteht aus 6 gleich großen Quadraten.
Jedes Quadrat hat einen Flächeninhalt von $ 16\,\mathrm{cm^2} .$
Berechnen Sie den Umfang des Rechtecks.
Max nimmt sich eine Kugel ohne hinzusehen.
Geben Sie die Wahrscheinlichkeit dafür an, dass diese Kugel dunkel ist.
Entscheiden Sie, welche Zuordnung proportional ist.
Lebensalter $ \longrightarrow $ Körpergröße
Eine Portion Pommes Frites kostet 1,20€. Drei Portionen kosten 3€.
| Anzahl Bockwürste | 2 | 4 | 10 |
| Kilokalorien | 455 | 910 | 2275 |
Streifendiagramm
Das Streifendiagramm ist noch nicht fertig. Es soll den Aufbau des menschlichen Körpers zeigen.
| H | K | M |
Welcher Anteil bleibt aufgrund der Tabelle insgesamt für Haut und Muskeln übrig?
Berechnen Sie.
Entnehmen Sie den Anteil für Haut und den für Muskeln aus dem Diagramm.
Vervollständigen Sie die Tabelle.
| Teil des Körpers | Anteil am Körpergewicht |
| Haut (H) | |
| Knochen (K) | 12% |
| Muskeln (M) | |
| Blut (B) | 9% |
| Organe (O) | 12% |
| Rest (R) | 17% |
Zeichnen Sie in den weißen Bereich des Diagramms die Anteile für Blut (B), Organe (O) und den Rest (R) ein.
Berechnen Sie, wie schwer die Organe eines $ 60\,\mathrm{kg} $ schweren Jugendlichen sind.
Kletterpark
Familie Klein besucht einen Kletterpark. Zur Familie gehören: Vater, Mutter, zwei Söhne (12 und 14 Jahre alt) und eine 6-jährige Tochter.
| Kletterpark Preise (Einzelticket 2,5 h) | |
| 1 Kind (bis 13 Jahre) | 13 € |
| 1 Kind (14 bis 17 Jahre) | 15 € |
| 1 Erwachsener | 18 € |
| Schnupperkarte (1 Runde) | 10 € |
Für eine Familienkarte bezahlt Familie Klein 61 €.
Berechnen Sie, wie viel Euro die Familie im Vergleich zu den Einzeltickets spart.
Herr Klein und seine Tochter möchten nur die Schnupperkarte nutzen.
Welcher der folgenden Rechenausdrücke ist geeignet das gesparte Geld auszurechnen?
A: $ (13\euro + 18\euro) - 2\cdot 10\euro $
B: $ (13\euro - 10\euro) + (18\euro - 10\euro) $
Der ältere Sohn klettert eine halbe Stunde länger.
Die Zuordnung Zeit $ \rightarrow $ Eintrittspreis soll proportional sein.
Berechnen Sie die Höhe der Nachzahlung.
Dreieck
Geben Sie die Koordinaten des Punktes B an.
Verbinden Sie die Punkte A, B und C zu einem Dreieck und messen Sie die Größe des Innenwinkels $ \alpha $ am Eckpunkt A.
Berechnen Sie den Flächeninhalt $ A $ des rechtwinkligen Dreiecks ABC.
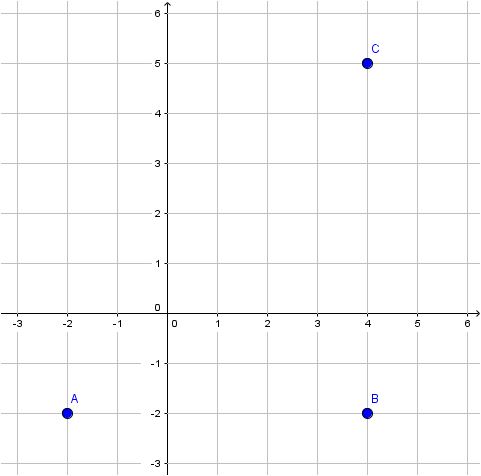
Berechnen Sie die Länge der Hypotenuse des Dreiecks ABC.
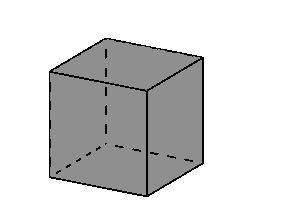
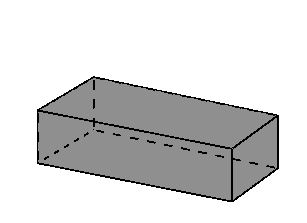
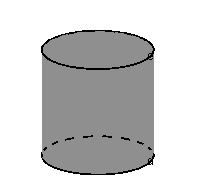
Körper
Ergänzen Sie die Tabelle.
|
|
|
| Name des Körpers | Zylinder | |
| Art der Grundfläche | Rechteck | |
| Anzahl der Flächen | 6 |
Von einem Zylinder ist die Größe der Grundfläche ($ A_G = 43\,\mathrm{cm^2} $) und die Länge der Höhe ($ h = 10\,\mathrm{cm} $) bekannt.
Geben Sie das Volumen des Zylinders an.
Wie groß ist der Radius des Zylinders?
$ 13,7\,\mathrm{cm} $
$ 4,3\,\mathrm{cm} $
$ 3,7\,\mathrm{cm} $
$ 6,6\,\mathrm{cm} $
Berechnen Sie die Oberfläche des Zylinders.
Glückskrad
Die Klasse 9a hat für das Schulfest ein Glücksrad mit 8 gleich großen Feldern gebaut. Es gewinnt die Zahl, auf deren Feld der Pfeil zeigt.
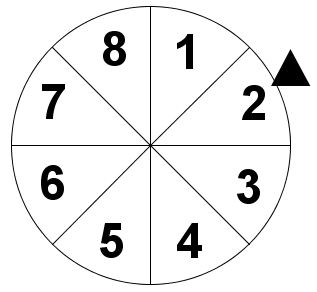
Entscheiden Sie, ob die folgenden Aussagen wahr oder falsch sind und begründen Sie.
(1) Die Wahrscheinlichkeit zu gewinnen ist für jede Zahl gleich groß.
(2) Die Wahrscheinlichkeit, dass die Zahl 8 gewinnt ist größer als die Wahrscheinlichkeit, dass die Zahl 4 gewinnt.
Wie groß ist die Wahrscheinlichkeit, eine gerade Zahl zu drehen?
Geben Sie die Wahrscheinlichkeit als Bruch und in Prozent an.
Berechnen Sie, wie groß die Wahrscheinlichkeit ist, zweimal hintereinander das Feld 4 zu drehen.
Kredit
Frau Stein möchte für ein Jahr einen Kredit in Höhe von $ 2200\euro $ aufnehmen. Der Zinssatz beträgt 7 %.
Berechne Sie, wie viel Euro Frau Stein zurückzahlen muss.
Bei einem anderem Geldinstitut müsste sie für dieselbe Kreditsumme $121\euro$ Zinsen im Jahr bezahlen.
Berechnen Sie die Höhe des Zinssatzes.
Schokolade
Eine Packung mit zwölf Schokoladentäfelchen enthält fünf Täfelchen mit Marzipanfüllung (M) und sieben Täfelchen Vollmilchschokolade (V). Zwei Schülerinnen nehmen ohne hinzusehen nacheinander je ein Täfelchen aus der Packung.
Zeichen Sie dafür ein Baumdiagramm. Tragen Sie die Ereignisse (M, V) und die zugehörigen Wahrscheinlichkeiten ein.
Berechnen Sie die Wahrscheinlichkeit, dass beide Schülerinnen ein Täfelchen mit Marzipanfüllung (M) ziehen.
Weitere Arbeitsblätter
Abschlussarbeit Klasse 9 ohne Taschenrechner
42 min, 11 Aufgaben #2851Aufgaben quer durch die 9. Klasse für Profis. Potenzrechnung, Terme, Gleichungen umstellen, Geometrie, Brüche, Maßstäbe, Funktionen und Kombinatorik. Alles ohne Taschenrechner! Auch als Vorbereitung auf den mittleren Schulabschluss (MSA) geeignet.
Extremwertaufgaben
80 min, 8 Aufgaben #1597Acht verschiedene Aufgaben mit immer derselben Fragen: wann wird's maximal bzw. minimal? Sei es mit einem Schiff, in einer Spielzeugfabrik, auf einer Wiese oder als Motorradfahrer: überall muss zuerst eine Hauptbedingung und eine Nebenbedingung aufgestellt und dann zusammen in eine Funktion gepackt werden. Letztlich wird von dieser dann jedes mal der Extrempunkt bestimmt.
Ebenengleichungen
22 min, 4 Aufgaben #1925Überblick aller drei Arten von Ebenengleichungen und wie man jeweils von einer Form in die andere kommt. Paramatergleichung, Normalengleichung und Koordinantengleichungen werden alle untereinander umgeformt.
Lineare Gleichungen
58 min, 5 Aufgaben #3738Einführung in das Umstellen von linearen Gleichungen. Die Aufgaben beginnen ganz einfach und werden dann nach und nach schwerer. Am Ende hat man gelernt: Klammern auflösen, links und rechts zusammenfassen, alles mit x auf die eine und alles ohne x auf die andere Seite. Zum Schluss noch durch die Zahl vor dem x teilen und fertig ist man.
Quadratische Gleichungen
74 min, 7 Aufgaben #0062Es werden zunächst quadratische Gleichungen sowohl über die Scheitelpunktsform als auch mit der pq-Formel gelöst. Im Anschluss gibt es Textaufgaben bei denen das Wissen benötigt wird.