Einleitung
Zwei originale Aufgaben der mittleren Schulabschluss Prüfung (MSA) von 2012 und 2014 aus Berlin.
14 Minuten Erklärungen in 2 Aufgaben von Koonys Schule.
Aufgaben
Der Vater von Max hat für den 18. Geburtstag im Garten ein Glücksrad aufgebaut. Für eine Spielrunde wird das Rad zweimal nacheinander gedreht.
Jedes Feld auf dem Glücksrad hat die gleiche Wahrscheinlichkeit.
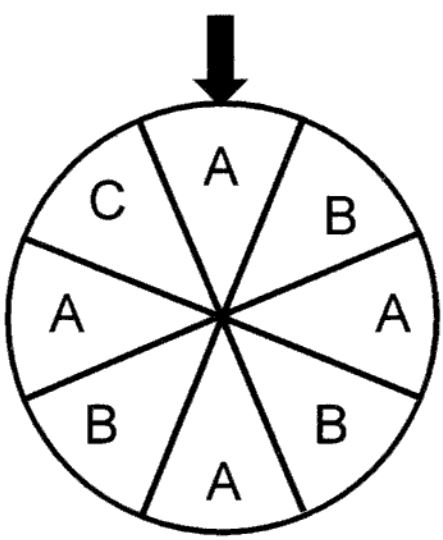
Ermitteln Sie die Wahrscheinlichkeit dafür, dass der Pfeil auf ein B zeigt.
Notieren Sie das Ergebnis als Bruch und in Prozent.
Zeichnen Sie ein Baumdiagramm für eine Spielrunde.
Berechnen Sie die Wahrscheinlichkeit dafür, dass der Pfeil zweimal nacheinander auf gleiche Buchstaben zeigt.
In einem Los-Topf befinden sich 250 Lose, darunter 5 Hauptgewinne und 50 kleinere Gewinne.
Alle anderen Lose sind Nieten.
Geben Sie an, wie groß die Wahrscheinlichkeit für das Ziehen einer Niete ist.
Max zieht zuerst nacheinander zwei Lose ohne sie zurückzulegen.
Vergleichen Sie die Wahrscheinlichkeiten für die zwei folgenden Ereignisse und notieren Sie Ihre Überlegungen:
$E_2$: Max zieht zwei kleine Gewinne.
Nachdem bereits 20 Lose, leider alles Nieten, aus dem Topf verkauft wurden, zieht ein Fremder nacheinander zwei Lose.
Herr und Frau Schmidt berechnen die Wahrscheinlichkeit für das Ereignis:
Beide haben falsch gerechnet.
Frau Schmidt: $\mathrm{P}(\mathrm{E_3}) = \frac{5}{230} \cdot \frac{175}{229}$
Herr Schmidt: $\mathrm{P}(\mathrm{E_3}) = \frac{5}{250} \cdot \frac{175}{249} + \frac{175}{250} \cdot \frac{5}{249}$
Erklären Sie, was die beiden falsch gemacht haben.
PDF zum Drucken
Lösungs-PDF
Weitere Arbeitsblätter
Lichtkunst Abitur GK Hamburg
61 min, 6 Aufgaben #1945Abituraufgabe aus der zentralen schriftlichen Abiturprüfung 2005 im Fach Mathematik aus Hamburg für den Grundkurs mit insgesamt 100 erreichbaren Punkten.
Strahlensätze *
27 min, 3 Aufgaben #4181Die Strahlensätze werden zunächst an klassischen Aufgaben mit gegebener Skizze gezeigt und im Anschluss an Textaufgaben gefestigt.
Kleine vermischte Übungen - Klasse 10
39 min, 13 Aufgaben #7400Bunt gemischte Textaufgaben zu verschiedenen Themen der 10. Klasse und darüber hinaus. Etwas zum Knobeln für Schüler am Anfang des Schuljahres.
Test über Vorkenntnisse zu ganzrationalen Funktionen
31 min, 4 Aufgaben #1515Originaler Test mit 40 erreichbaren Punkten.
Klausur - Grundkurs - 2. Semester
42 min, 3 Aufgaben #1660Originale Grundkurs Klausur aus Berlin eines 2. Semesters. Der Hauptteil ist die Kurvendiskussion einer e-Funktion. Wendetangente, Stammfunktion und Flächeninhalt inklusive. Die andere Hälfte beinhaltet Integralrechnung mit Parametern und ein paar kombinatorische Aufgaben.