Einleitung
Aufgaben zur Kombinatorik mit Sitzplätzen, Fußballturnieren, Silvester und defekten Batterien.
Man benötigt die Abzählverfahren (mit oder ohne Reihenfolge, mit oder ohne Wiederholung). Das Lotto-Modell und Gewinnerwartung sind auch dabei.
54 Minuten Erklärungen in 7 Aufgaben von Koonys Schule.
Aufgaben
An einem Tisch befinden sich 8 freie Sitzplätze. Auf wie viele Arten können sich 4 Personen auf diese Plätze verteilen?
Ein Eisenwarengeschäft führt Nägel in 8 verschiedenen Längen, die jeweils in 3 verschiedenen Stärken vorhanden sind, verzinkt und unverzinkt. Das Geschäft bietet jeweils 4 verschiedene Packungsgrößen an.
Wie viele verschiedene Angebotsvarianten gibt es?
Ein Vertreter möchte 8 Firmen besuchen. Wie viele verschiedene Variationen kann er für seine Fahrtroute wählen?
An einem Fußballturnier nehmen 8 Mannschaften teil. Wie viele Endspielkombinationen sind möglich?
In einer Stadt gibt es 5000 Telefonanschlüsse. Wie viele Gesprächspaarungen sind möglich?
Aus einer Klasse mit 25 Schülern sollen drei Schüler abgeordnet werden. Wie viele Gruppenzusammenstellungen sind möglich?
Wie groß ist die Wahrscheinlichkeit, dass man beim Lotto „6 aus 49“ mit einem abgegebenen Tipp genau vier Richtige erzielt?
Bei einer Silvester-Party stößt um Mitternacht jeder der 7 Party-Gäste mit dem Sektglas mit jedem Gast an. Wie oft klingen die Gläser?
Auf einem Rummelplatz wird ein Minilotto „4 aus 16“ angeboten. Der Spieleinsatz beträgt pro Tipp 1€. Die Auszahlungsquoten lauten 10€ bei 3 Richtigen und 1000€ bei 4 Richtigen. Mit welchem mittleren Gewinn kann der Veranstalter pro Tipp rechnen?
In einer Urne befinden sich 5 rote, 3 weiße und 6 schwarze Kugeln. 3 Kugeln werden ohne Zurücklegen gezogen. Mit welcher Wahrscheinlichkeit sind sie alle verschiedenfarbig (alle rot, alle gleichfarbig)?
In einer Sendung von 80 Batterien befinden sich 10 defekte. Mit welcher Wahrscheinlichkeit enthält eine Stichprobe von 5 Batterien genau eine (genau 3, höchstens 4, mindestens eine) defekte Batterie?
Weitere Arbeitsblätter
Rechnen mit Brüchen
53 min, 13 Aufgaben #066013 mal 5 Aufgaben zum Addieren, Subtrahieren, Multiplizieren und Dividieren von Brüchen. Täglich etwas machen und 2 Wochen später ist man besser. :)
Abschlussarbeit Klasse 9 mit Taschenrechner
42 min, 6 Aufgaben #2853Aufgaben quer durch die 9. Klasse. Statistiken, lineare Gleichungen, Funktionen, Textgleichungen, Strahlensätze, Prozentrechnung und Flächeninhalten. Auch als Vorbereitung auf den mittleren Schulabschluss (MSA) geeignet.
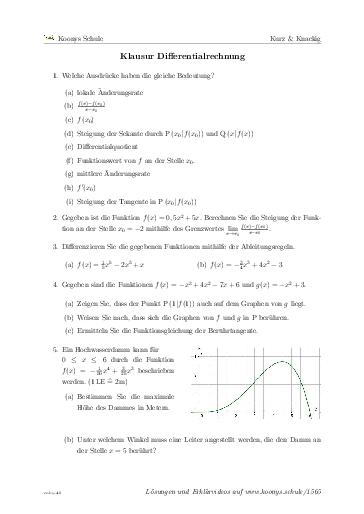
Klausur Differentialrechnung
42 min, 5 Aufgaben #1565Originale Klausur mit 38 Punkten. Das Verständnis zu den Begrifflichkeiten des Themas muss gezeigt, ein Grenzwert mit Hilfe des Differentialquotienten berechnen und Potenzfunktionen mit Ableitungsregeln differenziert (abgeleitet) werden. Zusätzlich kommt das Berührproblem und das Tangentenproblem sowie eine Anwendungsaufgabe vor.
Klassenarbeit binomische Formeln
33 min, 8 Aufgaben #3132Klassenarbeit einer 8. Klasse in Berlin aus dem Jahre 2015.
Bernoulli-Ketten
43 min, 4 Aufgaben #1700Es gibt vier grundlegende Aufgabentypen bei Bernoulli-Ketten. Diese werden hier einfach straightforward geübt.