Aufgabe
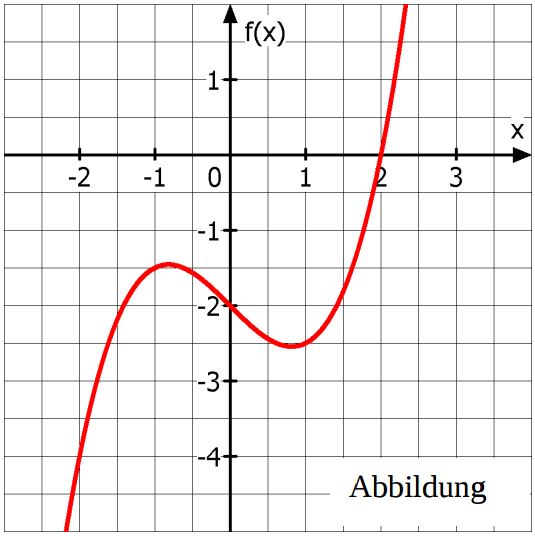
Gegeben ist die Funktion $f(x) = \frac{1}{2}x^3 - x- 2$. Der Graph ist in der Abbildung dargestellt.
Weisen Sie rechnerisch nach, dass die in der Zeichnung erkennbare Nullstelle tatsächlich eine Nullstelle ist.
Gegeben ist die Funktion $g_a(x) = f(x+a)$. Geben Sie an, wie sich der Graph von $g_a$ verändert, wenn man für a immer größere Zahlen einsetzt.
Geben Sie außerdem einen Wert für $ a $ an, so dass die Funktion $g_a$ die Nullstelle
$x=-1$ besitzt.
Arbeitsblatt mit dieser Aufgabe
Klausurvorbereitung - Analysis - NRW
15 min, 3 Aufgaben #1580Drei kleine verschiedene Aufgaben zur Differentialrechnung. Man muss Sachen berechnen und begründete Entscheidungen geben. Dafür werden Potenzfunktionen 3. Grades mit Nullstellen, Tangenten, Ableitungen und Verschiebungen von Funktionen benutzt.