Einleitung
Terme vereinfachen indem man gleichartige Glieder zusammenfasst und ggf. vorher noch ein paar Klammern auflöst.
Auch müssen Terme aufgestellt und Zahlenmauern gelöst werden.
43 Minuten Erklärungen in 8 Aufgaben von Koonys Schule.
Aufgaben
Vereinfache die Terme so weit wie möglich.
$ 3x+5x-4x $
$ 5a - 2a + a $
$ 4z^2 - 3z^2 + z^2 + 3z^2 $
$ 2,5xy + 1,5xy - 3xy $
$ -a^2z + 3a^2z $
$ 1,2xy^2 + 2,2y^2x - 1,5xy^2 + y^2x $
$ 3x+5y+x-7y-8y+11x $
$ 5xy - 2yz + 10xy - 2xz - 2yz $
$ 4 + 3a + 37 + 22,5a - 7,2 $
$ \frac{e^2}{2} + \frac{3f}{4} - \frac{1}{4}e^2 + 0,25f $
$ \left(\frac{1}{2}\right)^2x + 2^3y - \frac{5}{4}x + 2y - x $
$ 0,5^2ab - 0,25ab^2 + \frac{1}{4}ab^2 - ab $
$ 0,5a^2y + \frac{2}{6}a^2y^2 - \frac{1}{2}a\cdot ay - 0,5a^2y^2 $
$ \frac{1}{2}xy + \frac{1}{3}xz + 1\frac{1}{2}xy - \frac{4}{3}xz - \frac{5}{2}xy $
Löse die Klammern auf und fasse so weit wie möglich zusammen.
$ 8x + (3y+2x) $
$ a+(3a-b) $
$ -5z+(-3z+5) $
$ 7e+(-e-f) $
$ -8x+(3y+(-2x)) $
$ 2z+(5-(-2z)) $
Stelle einen Term zur Berechnung des Umfangs der Figur auf. Vereinfache den Term so weit wie möglich.
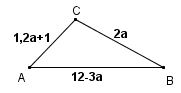
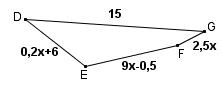
Weitere Arbeitsblätter
Teilweises Wurzelziehen - Rationalmachen des Nenners
52 min, 11 Aufgaben #0992Aufgaben zum teilweisen, auch partiellen, Wurzelziehen mit Zahlen, Variablen und Faktorisieren. Einfache Aufgaben zum Rationalmachen des Nenners.
Quadratische Gleichungen
74 min, 7 Aufgaben #0062Es werden zunächst quadratische Gleichungen sowohl über die Scheitelpunktsform als auch mit der pq-Formel gelöst. Im Anschluss gibt es Textaufgaben bei denen das Wissen benötigt wird.
Textgleichungen mit Brüchen für Profis 2v3
31 min, 7 Aufgaben #1342Textaufgaben müssen gelöst werden indem man Gleichungen aufstellt bei denen Brüche vorkommen.
Klausur - Grundkurs - 2. Semester
42 min, 3 Aufgaben #1660Originale Grundkurs Klausur aus Berlin eines 2. Semesters. Der Hauptteil ist die Kurvendiskussion einer e-Funktion. Wendetangente, Stammfunktion und Flächeninhalt inklusive. Die andere Hälfte beinhaltet Integralrechnung mit Parametern und ein paar kombinatorische Aufgaben.
Klassenarbeit Wachstum und Zerfall
38 min, 5 Aufgaben #6551Originale Klassenarbeit zum Thema Wachstum und Zerfall aus einem E-Kurs eines 10. Jahrgangs. Es wird auf den Unterschied von linearen und exponentiellen Wachstum eingegangen, Funktionsgleichungen aufgestellt, Graphen gezeichnet und Halbwertszeiten berechnet. Außerdem kommt prozentuale Ab- und Zunahme dran, sowie das Aufstellen einer Funktionsgleichung mit zwei Punkten als Zusatzaufgabe.