Einleitung
Originale Klausur mit 38 Punkten. Das Verständnis zu den Begrifflichkeiten des Themas muss gezeigt, ein Grenzwert mit Hilfe des Differentialquotienten berechnen und Potenzfunktionen mit Ableitungsregeln differenziert (abgeleitet) werden. Zusätzlich kommt das Berührproblem und das Tangentenproblem sowie eine Anwendungsaufgabe vor.
42 Minuten Erklärungen in 5 Aufgaben von Koonys Schule.
Aufgaben
Welche Ausdrücke haben die gleiche Bedeutung?
lokale Änderungsrate
$ \frac{f(x) - f(x_0)}{x-x_0} $
$ f(x_0) $
Steigung der Sekante durch $ \EPUNKT{P}{x_0}{f(x_0)} $ und $ \EPUNKT{Q}{x}{f(x)} $
Differentialquotient
Funktionswert von $ f $ an der Stelle $ x_0 $.
mittlere Änderungsrate
$ f'(x_0) $
Steigung der Tangente in $ \EPUNKT{P}{x_0}{f(x_0)} $
Gegeben ist die Funktion $ f(x) = 0,5x^2 + 5x $. Berechnen Sie die Steigung der Funktion an der Stelle $ x_0 = -2 $ mithilfe des Grenzwertes $ \lim\limits_{x\rightarrow x_0} \frac{f(x) - f(x_0)}{x-x_0} $.
Differenzieren Sie die gegebenen Funktionen mithilfe der Ableitungsregeln.
$ f(x) = \frac{1}{5} x^5 - 2x^3 + x $
$ f(x) = -\frac{3}{4} x^3 + 4x^2 - 3 $
Gegeben sind die Funktionen $ f(x) = -x^3 + 4x^2 - 7x + 6 $ und $ g(x) = -x^2 + 3 $.
Zeigen Sie, dass der Punkt $ \EPUNKT{P}{1}{f(1)} $ auch auf dem Graphen von $ g $ liegt.
Weisen Sie nach, dass sich die Graphen von $ f $ und $ g $ in P berühren.
Ermitteln Sie die Funktionsgleichung der Berührtangente.
Ein Hochwasserdamm kann für
$ 0 \le x \le 6 $ durch die Funktion $ f(x) = -\frac{1}{50}x^4 + \frac{3}{25}x^3 $ beschrieben werden. ($ 1\,\mathrm{LE} \equiv 2\,\mathrm{m} $)
(a) Bestimmen Sie die maximale Höhe des Dammes in Metern.
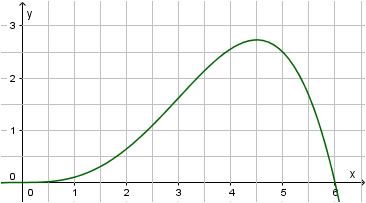
(b) Unter welchem Winkel muss eine Leiter angestellt werden, die den Damm an der Stelle $ x = 5 $ berührt?
PDF zum Drucken
Lösungs-PDF
Weitere Arbeitsblätter
Wochenübung mit Klammern und Gleichungen
29 min, 7 Aufgaben #12347 Aufgaben für 7 Tage. Es müssen Klammern aufgelöst, Terme zusammengefasst und vor allem Gleichungen gelöst werden. Dabei treten unter anderem auch mal Brüche, die binomischen Formeln und die pq-Formel mit auf.
Bernoulli-Ketten
43 min, 4 Aufgaben #1700Es gibt vier grundlegende Aufgabentypen bei Bernoulli-Ketten. Diese werden hier einfach straightforward geübt.
Textaufgaben mit mehreren Unbekannten
46 min, 11 Aufgaben #1336Elf Textaufgaben bei denen immer zunächst zwei Gleichungen mit zwei Unbekannten aufgestellt und dann gelöst werden müssen.
Smartphones Abitur GK Berlin 2016
44 min, 6 Aufgaben #1991Abituraufgabe zur analytischen Geometrie für den Grundkurs mit 30 erreichbaren Bewertungseinheiten aus Berlin 2016.
Binomische Formeln
89 min, 11 Aufgaben #3120Alles rund um die binomischen Formeln. Voraussetzung ist das Auflösen von doppelten Klammern (doppeltes Distributivgesetz). Darauf aufbauend wird auf das Vereinfachen von Termen eingegangen bei denen die binomischen Formeln von einfach bis schwer zur Anwendung kommen. Danach wird der Spieß umgedreht und Terme mit den binomischen Formeln faktorisiert. Krönender Abschluss bilden Gleichungen bei denen man ... *trommelwirbel* ... binomische Formeln braucht.