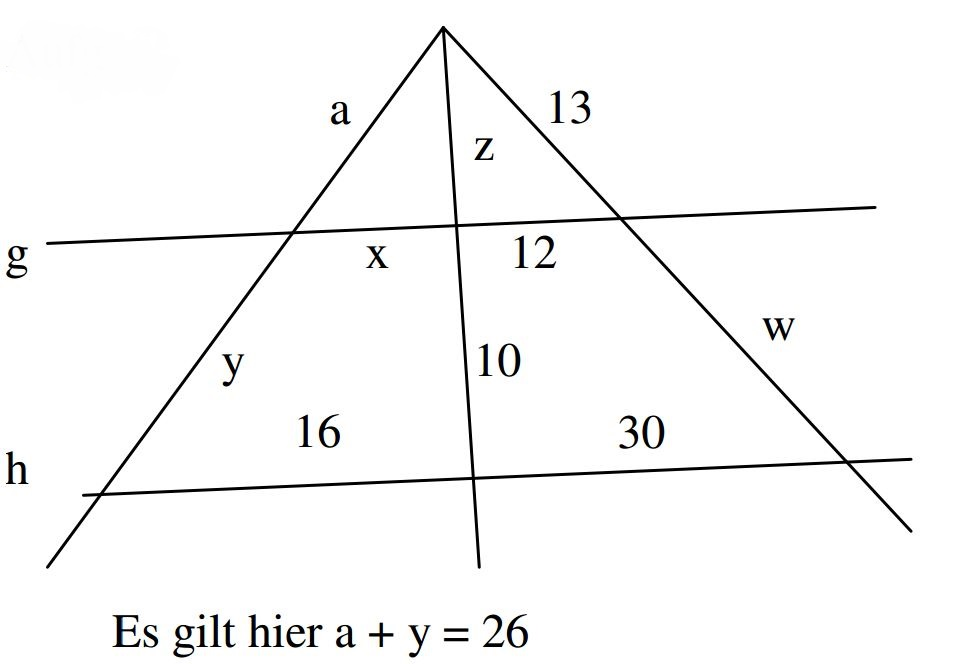
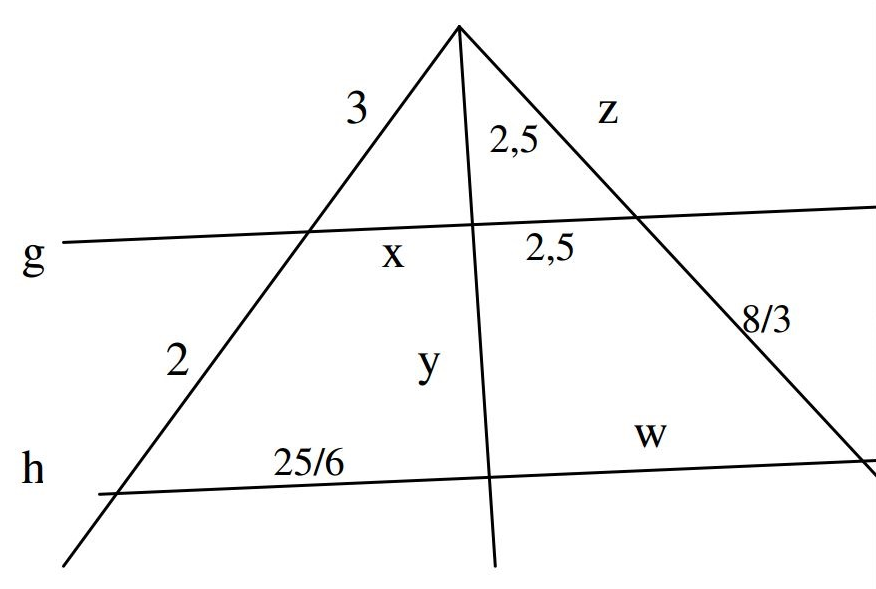
Einleitung
Drei Schenkel, verdrehte Skizzen, Erbsen und der Mond sowie Bergspitzen. Das Prinzip ist das Gleiche, aber die Schwierigkeit ist doch um einiges größer als sonst.
Das nächste Level an Strahlensatzaufgaben sozusagen.
54 Minuten Erklärungen in 6 Aufgaben von Koonys Schule.
Aufgaben
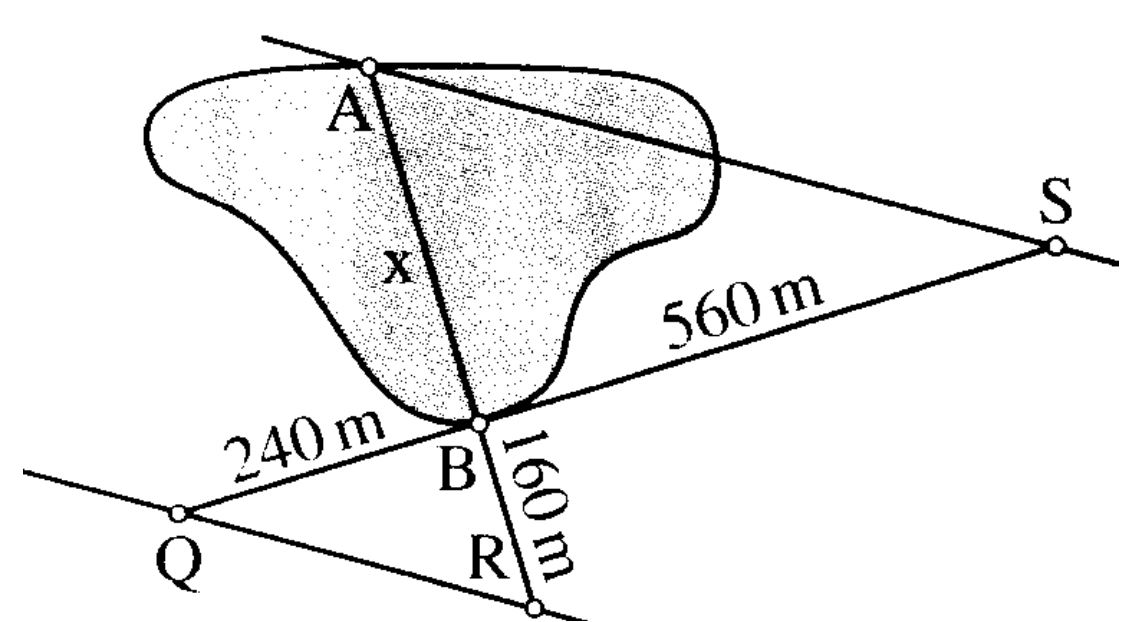
Zwei Geländepunkte A und B sind durch einen See getrennt. Ihr Abstand soll mit Hilfe geeignet gewählter Punkte Q, R und S bestimmt werden.
Worauf muss man bei diesem Verfahren unbedingt achten?
Bestimme den Abstand der Punkte A und B aus den in der nebenstehenden Abbildung gegebenen Angaben.
Eine Erbse von 6mm Durchmesser verdeckt gerade den 384\,000km entfernten Vollmond, wenn man sie 66cm vom Auge entfernt hält.
Wie groß ist der Monddurchmesser?
Ein Wanderer erblickt zwei Bergspitzen S und T.
Er hält sich einen Bleistift so vor ein Auge (das andere Auge macht er zu), sodass der Bleistift parallel zu $\overline{ST}$ liegt und die Bleistiftspitze A mit der Bergspitze S und das Bleistifende B mit der Bergspitze T jeweils in einer Blickrichtung liegt.
Wie weit ist der Wanderer vom Berg S entfernt, wenn die Entfernung der Bergspitzen $\overline{ST}$ = 25km, die Länge des Bleistifts $\overline{AB}$ = 20cm und die Entfernung der Bleistiftspitze A vom Auge 40cm beträgt.
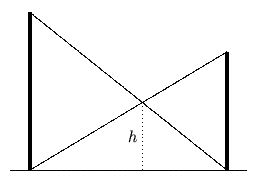
Die Seitenteile eines Regals sind 1,80m bzw. 1,50m lang. Zur Stabilisierung des Regals sollen zwei Diagonalstreben festgeschraubt werden. In welcher Höhe h treffen sich die beiden Streben?
Alle Erklärungen sind auch in einer
PDF zum Drucken
Lösungs-PDF
Weitere Arbeitsblätter
Kepler und Gravitation
81 min, 8 Aufgaben #6030Zwei Massen ziehen sich, je nach ihrer Entfernung voneinander, an. Eine Formel um auszurechnen wie stark gibt es natürlich auch. Damit einhergehend gibt es Aufgaben, die gelöst werden können. Zum Beispiel Geschwindigkeiten von Raketen und Satelliten oder die Masse der Sonne.
Klammern auflösen
56 min, 9 Aufgaben #3337Alle Möglichkeiten von Klammern auf einem Blatt. Mit diesen Übungen kann beim Auflösen von Klammern gar nichts mehr schief laufen.
Klassenarbeit Terme und Gleichungen
26 min, 5 Aufgaben #3750Klassenarbeit einer 8. Klasse auf einem Berliner Gymnasium. Es müssen Terme vereinfacht und Gleichungen gelöst werden. Dabei müssen Klammern aufgelöst, binomische Formeln angewendet und Gleichungen aus Texten aufgestellt werden.
Klassenarbeit - Rechnen mit Wurzeln
27 min, 9 Aufgaben #0993Originale Arbeit einer 9. Klasse mit 60 möglichen Punkten ohne Taschenrechner zur Wurzelrechnung.
Kleine vermischte Übungen - Klasse 10
39 min, 13 Aufgaben #7400Bunt gemischte Textaufgaben zu verschiedenen Themen der 10. Klasse und darüber hinaus. Etwas zum Knobeln für Schüler am Anfang des Schuljahres.