Einleitung
Aufgaben von leicht nach schwerer zum Üben.
61 Minuten Erklärungen in 10 Aufgaben von Mathe mit Rick und Koonys Schule.
Aufgaben
Berechne die folgenden unbestimmten Integrale.
$\int x^3\,\mathrm{d}x$
$\int x^4\,\mathrm{d}x$
$\int x^5\,\mathrm{d}x$
$\int m\cdot x^{10}\,\mathrm{d}x$
Berechnen Sie die folgenden unbestimmten Integrale.
$\int (x^3 + 5)\,\mathrm{d}x$
$\int (x^4 + 2)\,\mathrm{d}x$
$\int (x^5 - 1)\,\mathrm{d}x$
Berechne die unbestimmten Integrale.
$\int (x^3 + x)\,\mathrm{d}x$
$\int (x^4 + x^3)\,\mathrm{d}x$
$\int (x^5 - x)\,\mathrm{d}x$
Berechne die folgenden unbestimmten Integrale.
$\int (4x^3 + 2x)\,\mathrm{d}x$
$\int (2x^4 + 4x)\,\mathrm{d}x$
$\int (6x^3 - 6x^2)\,\mathrm{d}x$
Berechne die folgenden unbestimmten Integrale.
$ \int (2x^4+5x^3) \,\mathrm{d}x $
$ \int (6x^5-x^2) \,\mathrm{d}x $
$ \int (2x^4 - 2x^3) \,\mathrm{d}x $
Weitere Arbeitsblätter
BBR - Vergleichsarbeit Mathematik
59 min, 14 Aufgaben #2508Die Vergleichende Arbeit 2015 im Fach Mathematik zum Erwerb der Berufsbildungsreife bzw. des Hauptschulabschlusses. Bearbeitungszeit: 90 Minuten. Zugelassene Hilfsmittel: Formelübersicht und wissenschaftlicher nicht grafikfähiger Standard-Taschenrechner.
Anwendungsaufgaben Körper
13 min, 4 Aufgaben #9599Zusammengesetzte Aufgaben mit Zylindern, Kegeln und Kugeln bezüglich Volumen und Oberflächen. Kombiniert sind die Aufgaben mit Prozentrechnung, Dreisatz und Dichte.
Kreise - Anwendung
67 min, 6 Aufgaben #8889Flächen- und Umfangsformel des Kreises müssen in verschiedenen Aufgaben flexibel und mehrschrittig eingesetzt werden.
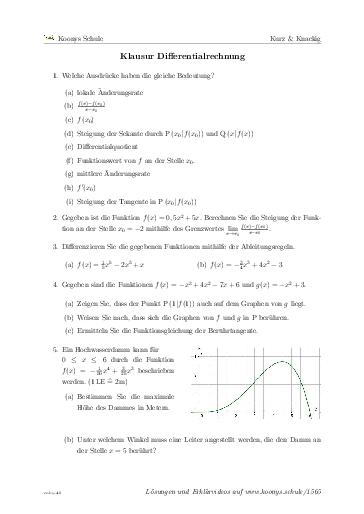
Klausur Differentialrechnung
42 min, 5 Aufgaben #1565Originale Klausur mit 38 Punkten. Das Verständnis zu den Begrifflichkeiten des Themas muss gezeigt, ein Grenzwert mit Hilfe des Differentialquotienten berechnen und Potenzfunktionen mit Ableitungsregeln differenziert (abgeleitet) werden. Zusätzlich kommt das Berührproblem und das Tangentenproblem sowie eine Anwendungsaufgabe vor.
Ebenengleichungen
22 min, 4 Aufgaben #1925Überblick aller drei Arten von Ebenengleichungen und wie man jeweils von einer Form in die andere kommt. Paramatergleichung, Normalengleichung und Koordinantengleichungen werden alle untereinander umgeformt.