Einleitung
Es gibt vier grundlegende Aufgabentypen bei Bernoulli-Ketten. Diese werden hier einfach straightforward geübt.
43 Minuten Erklärungen in 4 Aufgaben von Koonys Schule.
Aufgaben
Berechne die Trefferwahrscheinlichkeit dafür, dass bei n Durchgängen das Ergebnis mit der Wahrscheinlichkeit p genau k-mal eintritt.
n = 5, p = 30 %, k = 2
n = 9, p = 40 %, k = 5
n = 10, p = 30 %, k = 5
n = 5, p = 70 %, k = 2
n = 9, p = 60 %, k = 5
n = 10, p = 70 %, k = 5
Berechne die Trefferwahrscheinlichkeit dafür, dass bei n Durchgängen bis zu k-mal das Ergebnis mit der Wahrscheinlichkeit p eintrifft.
n = 12, p = 10 %, k = 3
n = 6, p = 20 %, k = 1
n = 8, p = 10 %, k = 3
n = 12, p = 90 %, k = 9
n = 6, p = 80 %, k = 5
n = 8, p = 90 %, k = 5
Berechne die Trefferwahrscheinlichkeit dafür, dass bei n Durchgängen das Ergebnis mit der Wahrscheinlichkeit p mindestens k-mal eintrifft.
n = 16, p = 40 %, k = 4
n = 11, p = 10 %, k = 11
n = 8, p = 20 %, k = 3
n = 16, p = 60 %, k = 4
n = 11, p = 90 %, k = 11
n = 8, p = 80 %, k = 3
Berechne die Trefferwahrscheinlichkeit dafür, dass bei n Durchgängen das Ergebnis mit der Wahrscheinlichkeit p mindestens $k_1$-mal und höchstens $k_2$-mal eintrifft.
n = 19, p = 40 %,
P(4$\le$X$\le$15)
n = 12, p = 20 %,
P(3$\le$X$\le$9)
n = 20, p = 10 %,
P(4$\le$X$\le$16)
n = 19, p = 60 %,
P(5$\le$X$\le$14)
n = 12, p = 80 %,
P(3$\le$X$\le$9)
n = 20, p = 90 %,
P(4$\le$X$\le$16)
Weitere Arbeitsblätter
Felder und Kreise - GK Klausur Physik
40 min, 3 Aufgaben #6123Originale Physik Klausur für einen Grundkurs im 2. Semester aus Berlin. 39 Punkte, 90min
Teilweises Wurzelziehen - Rationalmachen des Nenners
52 min, 11 Aufgaben #0992Aufgaben zum teilweisen, auch partiellen, Wurzelziehen mit Zahlen, Variablen und Faktorisieren. Einfache Aufgaben zum Rationalmachen des Nenners.
Anwendungsaufgaben radioaktiver Zerfall
58 min, 5 Aufgaben #6543Textaufgaben über Stoffe, die exponentiell Zerfallen. Wertetabellen, Prozente und Halbwertszeiten kommen unter anderem vor. Es sind im Wesentlichen verschiedene Aufgaben zu Exponentialfunktionen deren Wachstumsfaktor kleiner als 1 ist.
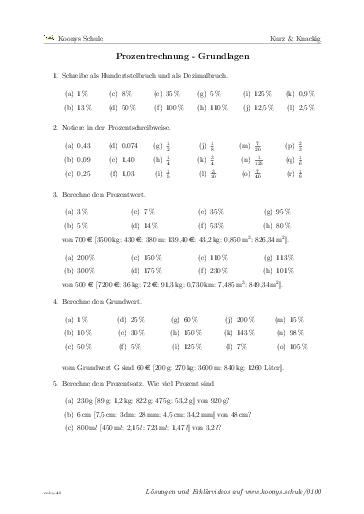
Prozentrechnung - Grundlagen
81 min, 5 Aufgaben #0100Hier geht es um pures Rechnen. Zunächst wird der Zusammenhang von Prozenten und Brüchen geübt und im Anschluss die drei grundlegenden Aufgabentypen der Prozentrechnung.
Klammern auflösen
56 min, 9 Aufgaben #3337Alle Möglichkeiten von Klammern auf einem Blatt. Mit diesen Übungen kann beim Auflösen von Klammern gar nichts mehr schief laufen.