Einleitung
Typische Aufgaben der Wahrscheinlichkeitsrechnung für die Sekundarstufe. Mit dabei sind Ergebnismengen, Baumdiagramme und Gewinnerwartung. Natürlich auch Urnen, viele Kugeln und Lotterielose.
36 Minuten Erklärungen in 4 Aufgaben von Koonys Schule.
Aufgaben
In einer Urne befinden sich vier gleichartige Kugeln, die die Buchstaben A, B, C und D tragen. Aus der Urne werden zwei Kugeln nacheinander gezogen. Jede Kugel wird sofort nach ihrer Ziehung wieder zurückgelegt.
Zeichne das zugehörige Baumdiagramm. Gib die Ergebnismenge S an und berechne die Wahrscheinlichkeit für die folgenden Ereignisse:
$\mathrm{E_1}$: Die erste Kugel trägt den Buchstaben A, die zweite den Buchstaben B.
$\mathrm{E_2}$: Die erste Kugel trägt den Buchstaben D, die zweite den Buchstaben A.
$\mathrm{E_3}$: Die zweite Kugel trägt den Buchstaben D.
$\mathrm{E_4}$: Die zweite Kugel trägt den Buchstaben B.
In einer Urne befinden sich acht schwarze und vier gelbe gleichartige Kugeln. Es werden nacheinander drei Kugeln gezogen. Die Farbe jeder Kugel wird notiert, die Kugeln werden nicht wieder in die Urne zurückgelegt.
Gib die Ergebnismenge S an und berechne die Wahrscheinlichkeiten aller Ergebnisse.
Gib die folgenden Ereignisse jeweils als Teilmenge von S an und berechne ihre Wahrscheinlichkeiten.
$\mathrm{E_1}$: Es werden genau zwei gelbe Kugeln gezogen.
$\mathrm{E_2}$: Es werden genau drei schwarze Kugeln gezogen.
$\mathrm{E_3}$: Es werden höchstens zwei gelbe Kugeln gezogen.
$\mathrm{E_4}$: Es wird mindestens eine schwarze Kugel gezogen.
In einer Warensendung befinden sich zehn funktionsfähige (f) und vier defekte (d) elektronische Bauteile. Ein funktionsfähiges elektronisches Bauteil soll herausgefunden werden.
Berechne die Wahrscheinlichkeit dafür, dass höchstens drei elektronische Bauteile getestet werden müssen, um ein funktionsfähiges Bauteil zu erhalten.
Wie viele Bauteile müssen der Warensendung höchstens entnommen werden, um ein funktionsfähiges Bauteil zu erhalten? Berechne die Wahrscheinlichkeit für diesen Fall.
Bei einer Lotterie gewinnen 1% der Lose 10€, 2% der Lose 5€, 3% der Lose 2€ und 4% der Lose 1€. Die restlichen Lose sind Nieten. Jedes Los kostet 0,50€.
Welchen Gewinn kannst du erwarten, wenn du 200 Lose kaufst?
Wie viel Euro muss ein Los kosten, wenn der Lotterieveranstalter im Mittel pro Los 0,70€ verdienen will?
PDF zum Drucken
Lösungs-PDF
Weitere Arbeitsblätter
Einführung Terme
65 min, 8 Aufgaben #2826Erste Aufgaben zu Termen. Termwerte berechen, Terme vergleichen und Textgleichungen in beide Richtungen: sowohl Gleichungen aus Texten aufstellen aber auch Texte basierend auf Gleichungen verfassen. Die Hälfte der Aufgaben beschäftigt sich mit dem Zusammenfassen von Termen.
Klassenarbeit - Rechnen mit Wurzeln
27 min, 9 Aufgaben #0993Originale Arbeit einer 9. Klasse mit 60 möglichen Punkten ohne Taschenrechner zur Wurzelrechnung.
Klammern auflösen
35 min, 8 Aufgaben #3336Das Vereinfachen von Termen mit Klammern wird Stück für Stück gezeigt. Mit dabei sind Minusklammern, das einfache und das doppelte Distributivgesetz. Nach den Aufgaben ist man fachlich soweit sich als nächstes an die binomischen Formeln vagen zu können.
Klausur Differentialrechnung
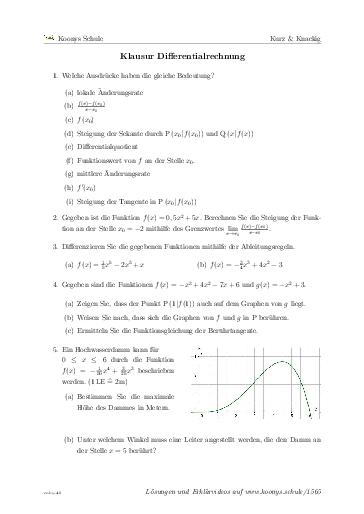
42 min, 5 Aufgaben #1565Originale Klausur mit 38 Punkten. Das Verständnis zu den Begrifflichkeiten des Themas muss gezeigt, ein Grenzwert mit Hilfe des Differentialquotienten berechnen und Potenzfunktionen mit Ableitungsregeln differenziert (abgeleitet) werden. Zusätzlich kommt das Berührproblem und das Tangentenproblem sowie eine Anwendungsaufgabe vor.
Ikarus Abitur GK Berlin 2016
64 min, 6 Aufgaben #1980Abituraufgabe zur analytischen Geometrie für den Grundkurs mit 30 erreichbaren Bewertungseinheiten aus Berlin 2016.