Einleitung
Originale Physik Klausur für einen Grundkurs im 2. Semester aus Berlin.
39 Punkte, 90min
40 Minuten Erklärungen in 3 Aufgaben von Koonys Schule.
Aufgaben
Elektrische und magnetische Felder
In welche Richtung wird der durch die anliegende Hochspannung beschleunigte Elektronenstrahl vom Dauermagneten in der rechts abgebildeten Kathodenstrahlröhre (Braun'sche Röhre) abgelenkt?
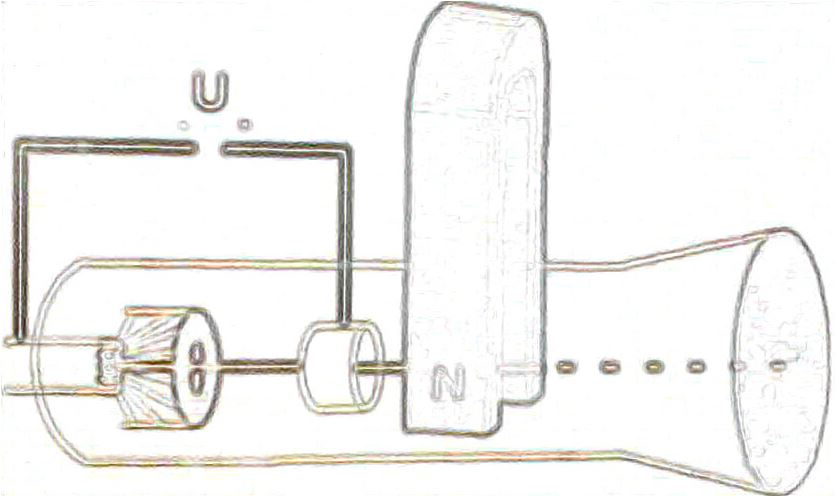
Betrachten Sie einen Elektronenstrahl im Vakuum, der durch ein beliebig großes homogenes Magnetfeld verläuft. Erklären Sie, warum die Elektronen sich auf einer Kreisbahn bewegen.
Die Kreisbahn aus 1b) habe den Radius $r = 31\,\mathrm{cm}$, die Bahngeschwindigkeit der Elektronen sei $v = 6\cdot 10^5 \frac{m}{s}$.
Welchen Betrag hat die magnetische Feldstärke $B$?
Wechselstromkreise
Zeichnen Sie das Schaltbild einer Reihenschaltung aus einer Wechselspannungsquelle, einer Spule, einem Kondensator, einem ohmschen Widerstand und einem Amperemeter.
Die Spannungsquelle liefert eine Wechselspannung der Frequenz $f = 500\,\mathrm{Hz}$ mit einer Effektivspannung von $U_{eff} = 100\,\mathrm{V}$, die Kapazität beträgt $C = 50\,\mathrm{nF}$, die Spule hat die Induktivität $L = 9\,\mathrm{mH}$ und der Widerstand beträgt $R = 120\,\mathrm{\Omega}$. Berechnen Sie die Effektivstromstärke in diesem Stromkreis.
Für welche Frequenz ist die Stromstärke maximal (d.h. der Widerstand minimal)?
Schwingkreis
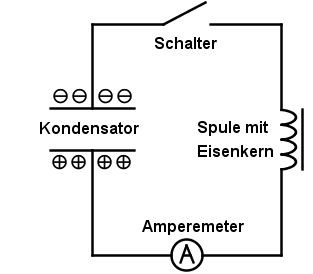
Die Skizze rechts stellt einen Stromkreis dar, der im Wesentlichen aus einer Spule und einem geladenen Kondensator besteht. Beschreiben und erläutern Sie den Vorgang, der nach dem Schließen des Schalters stattfindet.
Die (ideale) Spule habe eine Induktivität von $20\,\mathrm{mH}$. Berechnen Sie, welche Kapazität der Kondensator haben muss, damit der Schwingkreis mit der Frequenz $f = 880\,\mathrm{Hz}$ schwingt.
Weitere Arbeitsblätter
Strahlensätze **
54 min, 6 Aufgaben #4182Drei Schenkel, verdrehte Skizzen, Erbsen und der Mond sowie Bergspitzen. Das Prinzip ist das Gleiche, aber die Schwierigkeit ist doch um einiges größer als sonst. Das nächste Level an Strahlensatzaufgaben sozusagen.
Sinus - Kosinus - Tangens
41 min, 6 Aufgaben #7000Sinus, Kosinus und Tangens von leicht bis schwer. Zunächst Aufgaben mit den Gleichungen und all ihren Varianten. Danach Standard-Aufgaben an rechtwinkligen Dreiecken und die zweite Hälfte sind Textaufgaben bei denen das gleiche noch einmal drankommt mit dem gewissen Etwas, das anspruchsvolle Aufgaben ausmacht.
Wichtige Formeln im Gebäudeenergiegesetz
0 min, 4 Aufgaben #PQUVIn diesem Arbeitsblatt werden die grundlegenden Formeln zur Berechnung der wichtigsten Kennzahlen im Gebäudeenergiegesetz (GEG) vorgestellt. Sie erhalten die notwendigen Formeln und Erklärungen, um den Primärenergiebedarf, den Transmissionswärmeverlust, den Erneuerbare-Energien-Anteil und den U-Wert zu verstehen und anzuwenden. Diese Kennzahlen sind entscheidend für die Beurteilung der Energieeffizienz von Gebäuden und für die Umsetzung der Vorgaben des GEG.
Übungsaufgaben zur Stochastik
30 min, 6 Aufgaben #1654Die ersten fünf Aufgaben fragen danach, wie viele Elemente oder Möglichkeiten es gibt, und sind damit klassische Aufgaben zu Abzählverfahren (Kombinatorik). Die letzte Aufgabe beschäftigt sich mit Baumdiagrammen und Bernoulli-Ketten.
Studienkolleg Vektoren, SS 2017
127 min, 10 Aufgaben #1818Übungsblatt der Hochschule Kaiserslautern, University of Applied Sciences, zum Thema Vektoren.