Einleitung
Aufgaben quer durch die 9. Klasse.
Statistiken, lineare Gleichungen, Funktionen, Textgleichungen, Strahlensätze, Prozentrechnung und Flächeninhalten.
Auch als Vorbereitung auf den mittleren Schulabschluss (MSA) geeignet.
42 Minuten Erklärungen in 6 Aufgaben von Koonys Schule.
Aufgaben
Die Ergebnisse einer Klassenarbeit sind in der folgenden Tabelle dargestellt.
| Zensur | 1 | 2 | 3 | 4 | 5 | 6 |
| Klasse 9a | 3 | 6 | 7 | 6 | 2 | 1 |
| Klasse 9b | 2 | 6 | 10 | 3 | 2 | 1 |
Veranschauliche die Ergebnisse der Klasse 9a in einem sinnvollen Diagramm.
Ermittle für jede der beiden Klassen den Klassendurchschnitt, den Modalwert und den Zentralwert.
Löse die folgenden Gleichungen und führe jeweils eine Probe durch.
$ (7+x)\cdot 4 = 44 $
$ 3x\cdot (7+x) - (2x+3) = 3x^2 - 2x + 4 $
Durch die Gleichungen $ y = f(x) = x^2 - 2x $ und $ y = g(x) = -x+2 $ sind zwei Funktionen gegeben.
Stelle die beiden Funktionen im gleichen Koordinatensystem dar.
Lies die Nullstellen und die gemeinsamen Punkte beider Graphen ab.
Berechne ihre Nullstellen.
Gesucht sind zwei Zahlen, deren Summe 4 beträgt. Wird das Dreifache der einen Zahl um das Doppelte der anderen Zahl vermindert, so erhält man 52. Wie heißen die beiden Zahlen?
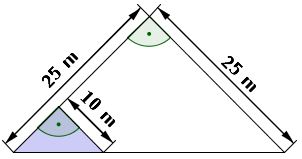
Von einem Grundstück in Form eines rechtwinklig-gleichschenkligen Dreiecks wird das gekennzeichnete Stück verkauft, das ebenfalls wieder ein rechtwinklig-gleichschenkliges Dreieck ist.
Um wie viel Prozent wird das ursprüngliche Grundstück dadurch kleiner?
Ein ein quadratisches Blech mit einer Seitenlänge von $ 5\,\mathrm{cm} $ soll genau in die Mitte ein Loch geschnitten werden, das ebenfalls die Form eines Quadrates und einen Flächeninhalt von $ 9\,\mathrm{cm^2} $ hat. Der verbleibende Streifen soll überall gleich breit sein.
Fertige eine Skizze an und trage die bekannten Stücke ein.
Welche Seitenlänge hat das herauszuschneidende Quadrat?
Wie viel Prozent wird von dem Ausgangsquadrat entfernt?
Weitere Arbeitsblätter
Aus 3 mach 4 - Abitur GK Berlin 2008
23 min, 5 Aufgaben #1987Original Abiturprüfung aus Berlin für den Grundkurs mit einem Glücksspielautomat. Mit dabei war die Kombinatorik, stochastische Unabhängigkeit, Bernoulli-Ketten, mindestens-mindestens Aufgabe und ein Hypothesentest.
Klammern auflösen
35 min, 8 Aufgaben #3336Das Vereinfachen von Termen mit Klammern wird Stück für Stück gezeigt. Mit dabei sind Minusklammern, das einfache und das doppelte Distributivgesetz. Nach den Aufgaben ist man fachlich soweit sich als nächstes an die binomischen Formeln vagen zu können.
Vermischte Übungen MSA
36 min, 6 Aufgaben #1290Textgleichungen, Gleichungen mit vielen Klammern, Gleichungssysteme, Textaufgaben zu Körperberechnungen und Wahrscheinlichkeiten sind Inhalt dieses Arbeitsblattes. Anspruchsvolle Aufgaben quer durchs Beet.
Anwendungsaufgaben Körper
13 min, 4 Aufgaben #9599Zusammengesetzte Aufgaben mit Zylindern, Kegeln und Kugeln bezüglich Volumen und Oberflächen. Kombiniert sind die Aufgaben mit Prozentrechnung, Dreisatz und Dichte.