Einleitung
Aufgaben quer durch die 9. Klasse.
Statistik, Diagramme, Volumenberechnungen am Kegel, Funktionen und mehr im Koordinatensystem.
Auch als Vorbereitung auf den mittleren Schulabschluss (MSA) geeignet.
38 Minuten Erklärungen in 3 Aufgaben von Koonys Schule.
Aufgaben
Die folgende Tabelle zeigt den Wasserverbrauch eines Vier-Personen-Haushaltes in den Jahren 2000 und 2005.
| Jahr | Körperpflege | Toilette | Wäsche | Geschirr | Putzen | Sonstiges |
| 2000 | $ 106,56\,\mathrm{cm^3} $ | $ 83,52\,\mathrm{m^3} $ | $ 31,68\,\mathrm{m^3} $ | $ 28,80\,\mathrm{m^3} $ | $ 20,16\,\mathrm{m^3} $ | $ 17,28\,\mathrm{m^3} $ |
| 2005 | $ 91,84\,\mathrm{m^3} $ | $ 56,00\,\mathrm{m^3} $ | $ 29,12\,\mathrm{m^3} $ | $ 17,92\,\mathrm{m^3} $ | $ 15,68\,\mathrm{m^3} $ | $ 13,44\,\mathrm{m^3} $ |
Um wie viel Prozent liegt der Wasserverbrauch der Familie im Jahr 2005 unter dem des Jahres 2000?
Vergleiche die Anteile für die Toilettenbenutzung bezüglich des Gesamtverbrauches in den beiden Jahren.
Stelle die Anteile für den Wasserverbrauch des Jahres 2005 in einem Diagramm dar.
Zwei Lkw-Ladungen mit grobkörnigem Kies wurden zu einem kegelförmigen Haufen mit einer Höhe von $ 1,40\,\mathrm{m} $ und einem Grundkreisdurchmesser von $ 3,80\,\mathrm{m} $ aufgeschüttet.
Wie viel Kubikmeter Kies hatte eine Lkw-Ladung?
Bei einer zweiten Lieferung wurde die Höhe des Kieshaufens um $ 0,40\,\mathrm{m} $ größer. Der Grundflächendurchmesser vergrößert sich ebenfalls entsprechend der Zeichnung.
Wie viel Kubikmeter Kies sind bei der zweiten Lieferung dazu gekommen?
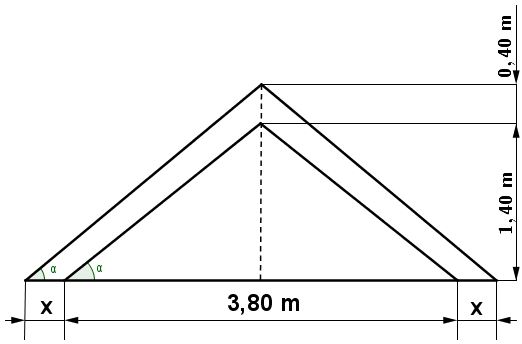
Berechne die Größe des Winkels $ \alpha $.
Zeichne im Intervall von $ 0 \le x \le 5 $ die beiden Funktionen $ y = f(x) = -x+2 $ und $ y = g(x) = (x-3)^2 - 3 $ in ein und dasselbe Koordinatensystem.
Gib die Koordinaten der Schnittpunkte $ A $ und $ B $ an.
Berechne die Länge der Strecke $ \overline{AB} $.
Spiegele $ \overline{AB} $ an der y-Achse. Es entsteht $ \overline{A'B'} $. Welches spezielle Viereck ist $ B'BAA' $?
Berechne den Umfang und den Flächeninhalt des Vierecks $ B'BAA' $.
Alle Erklärungen sind auch in einer
PDF zum Drucken
Lösungs-PDF
Weitere Arbeitsblätter
kgV und ggT
50 min, 6 Aufgaben #0010Primfaktorzerlegung, größter gemeinsamer Teiler und kleinstes gemeinsames Vielfaches nimmt die Hälfte des Blattes ein. Die andere Hälfte sind Anwendungsaufgaben.
Sinus - Kosinus - Tangens
41 min, 6 Aufgaben #7000Sinus, Kosinus und Tangens von leicht bis schwer. Zunächst Aufgaben mit den Gleichungen und all ihren Varianten. Danach Standard-Aufgaben an rechtwinkligen Dreiecken und die zweite Hälfte sind Textaufgaben bei denen das gleiche noch einmal drankommt mit dem gewissen Etwas, das anspruchsvolle Aufgaben ausmacht.
Aus 3 mach 4 - Abitur GK Berlin 2008
23 min, 5 Aufgaben #1987Original Abiturprüfung aus Berlin für den Grundkurs mit einem Glücksspielautomat. Mit dabei war die Kombinatorik, stochastische Unabhängigkeit, Bernoulli-Ketten, mindestens-mindestens Aufgabe und ein Hypothesentest.
Quadratische Gleichungen Ohne PQ-Formel
40 min, 5 Aufgaben #0060Die Aufgaben führen schrittweise an das Lösen von reinquadratischen Gleichungen verschiedener Formen heran.
Abschlussarbeit Klasse 9 ohne Taschenrechner
39 min, 8 Aufgaben #2850Aufgaben quer durch die 9. Klasse für Profis. Ohne Taschenrechner knifflige Terme berechnen. Außerdem Prozentrechnung, Flächeninhalte, Gleichungen umstellen, Funktionen, Textgleichungen, Strahlensätze und Wahrscheinlichkeiten. Auch als Vorbereitung auf den mittleren Schulabschluss (MSA) geeignet.