Einleitung
Verschiedene Übungen zu Ebenen.
Ebenen mit Spurgeraden zeichnen, Koordinatengleichungen von Ebenen mit verschiedenen Angaben bestimmen, Schnittgeraden, Abstand Punkt Gerade und Verständnisfragen.
52 Minuten Erklärungen in 6 Aufgaben von Koonys Schule.
Aufgaben
Zeichne die folgenden Ebenen mit Hilfe ihrer Spurgeraden in ein kartesisches Koordinatensystem ein:
E: $3x_1 + 4x_2 + 3x_3 = 12$
E: $2x_1 + 4x_2 = 8$
E: $x_2 = 3$
Bestimme jeweils eine Koordinatengleichung der Ebene E.
$\RPUNKT{A}{2}{2}{2},\, \RPUNKT{B}{4}{1}{3},\,\RPUNKT{C}{8}{4}{5}$
$\RPUNKT{A}{4}{1}{2},\, \mathrm{g:}\,\, \vec{x} = \RVEKTOR{c}{3}{5}{7} + t\cdot \RVEKTOR{c}{1}{1}{1}$
$\mathrm{g:}\,\,\vec{x} = \RVEKTOR{c}{1}{0}{2} + s\cdot \RVEKTOR{c}{3}{1}{2}$, $\mathrm{h:}\,\,\vec{x} = \RVEKTOR{c}{3}{3}{7} + t\cdot \RVEKTOR{c}{2}{1}{3}$
$\mathrm{g:}\,\,\vec{x} = \RVEKTOR{c}{1}{0}{2} + s\cdot \RVEKTOR{c}{3}{1}{2}$, $\mathrm{h:}\,\,\vec{x} = \RVEKTOR{c}{4}{1}{1} + t\cdot \RVEKTOR{c}{6}{2}{4}$
Die Ebene E ist Spiegelebene zwischen $\RPUNKT{A}{1}{4}{7}$ und $\RPUNKT{A^*}{3}{2}{3}$.
Die Ebene E enthält die Gerade $\vec{x} = \RVEKTOR{c}{3}{1}{2} + s \cdot \RVEKTOR{c}{2}{0}{-1}$ und ist orthogonal zur Ebene $\mathrm{F:} - x_1 + x_2 + 2x_3 + 2 = 0$.
Bestimme eine Gleichung der Schnittgeraden der Ebenen $\mathrm{E:} x_1 - x_2 + 2x_3 = 7$ und $\mathrm{F:} -x_1 + x_2 + 2x_3 + 2 = 0$.
Berechne den Abstand des Punktes $\RPUNKT{R}{6}{9}{4}$ von der Ebene
$\mathrm{E:}\left[\vec{x} - \RVEKTOR{c}{7}{5}{2}\right]\cdot \RVEKTOR{c}{2}{2}{1} = 0$.
Gegeben seien die Gerade g und die Ebene E durch $\mathrm{g:}\,\vec{x} = \vec{a} + t\cdot \vec{r},\,\,t\in \RR $ und $\mathrm{E:}\,\left(\vec{x} - \vec{b}\right)\cdot \vec{n} = 0$.
Welche geometrische Bedeutung haben die Vektoren $\vec{a}$, $\vec{b}$, $\vec{r}$, $\vec{n}$ und $\left(\vec{x} - \vec{b}\right)$?
Welche Beziehung muss zwischen den Vektoren gelten, damit gilt
g ist parallel zu E
g ist orthogonal zu E
g liegt in E
Alle Erklärungen sind auch in einer
PDF zum Drucken
Lösungs-PDF
Weitere Arbeitsblätter
Kepler und Gravitation
81 min, 8 Aufgaben #6030Zwei Massen ziehen sich, je nach ihrer Entfernung voneinander, an. Eine Formel um auszurechnen wie stark gibt es natürlich auch. Damit einhergehend gibt es Aufgaben, die gelöst werden können. Zum Beispiel Geschwindigkeiten von Raketen und Satelliten oder die Masse der Sonne.
Strahlensätze **
54 min, 6 Aufgaben #4182Drei Schenkel, verdrehte Skizzen, Erbsen und der Mond sowie Bergspitzen. Das Prinzip ist das Gleiche, aber die Schwierigkeit ist doch um einiges größer als sonst. Das nächste Level an Strahlensatzaufgaben sozusagen.
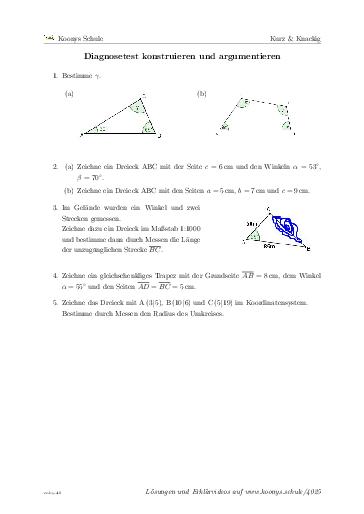
Diagnosetest konstruieren und argumentieren
36 min, 5 Aufgaben #4025Aufgaben zur Konstruktion von Dreiecken mit Hilfe der Kongruenzsätze. Außerdem kommen Innenwinkelsatz, ein gleichschenkliges Trapez und die Konstruktion des Umkreises eines Dreiecks im Koordinatensystem vor.
Vermischte Übungen MSA
36 min, 6 Aufgaben #1290Textgleichungen, Gleichungen mit vielen Klammern, Gleichungssysteme, Textaufgaben zu Körperberechnungen und Wahrscheinlichkeiten sind Inhalt dieses Arbeitsblattes. Anspruchsvolle Aufgaben quer durchs Beet.
Wurzelterme vereinfachen ohne Taschenrechner
41 min, 13 Aufgaben #0990Viele verschiedene Aufgaben zum Zusammenfassen von Wurzeltermen. Dabei werden neben den Wurzelgesetzen auch binomische Formeln benötigt.