Einleitung
Beispielaufgaben für die zentralen Klausuren aus Nordrhein-Westfalen vom Schulministerium.
Es wird vor allem das Verständnis der Ableitungsfunktion geprüft. Wachstumsgeschwindigkeiten, Funktionsgleichungen von Tangenten und Skizzen kommen vor.
16 Minuten Erklärungen in 3 Aufgaben von Koonys Schule.
Aufgaben
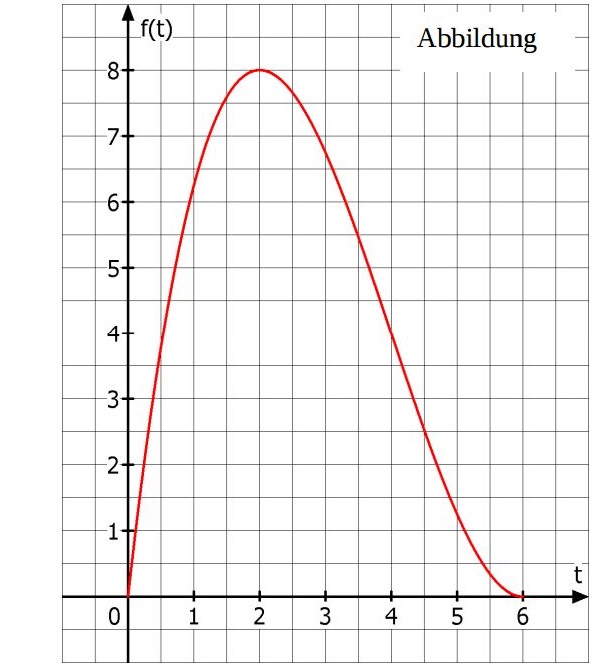
Die Funktion $f(t) = \frac{1}{4}t^3 - 3t^2+9t$ beschreibt näherungsweise die Wachstums geschwindigkeit einer Pflanze in der Einheit Zentimeter pro Woche. Dabei gibt $t$ die Zeit in Wochen seit Beobachtungsbeginn an, es gilt: $0 \le t \le 6$. Der Graph der Funktion ist in der Abbildung dargestellt.
Berechnen Sie die Wachstumsgeschwindigkeit der Pflanze nach zwei Wochen.
Nehmen Sie an, die Pflanze hätte nach vier Wochen eine Höhe von 70cm.
Entscheiden Sie begründet, ob die Pflanze nach fünf Wochen kleiner, größer oder gleich 74cm ist.
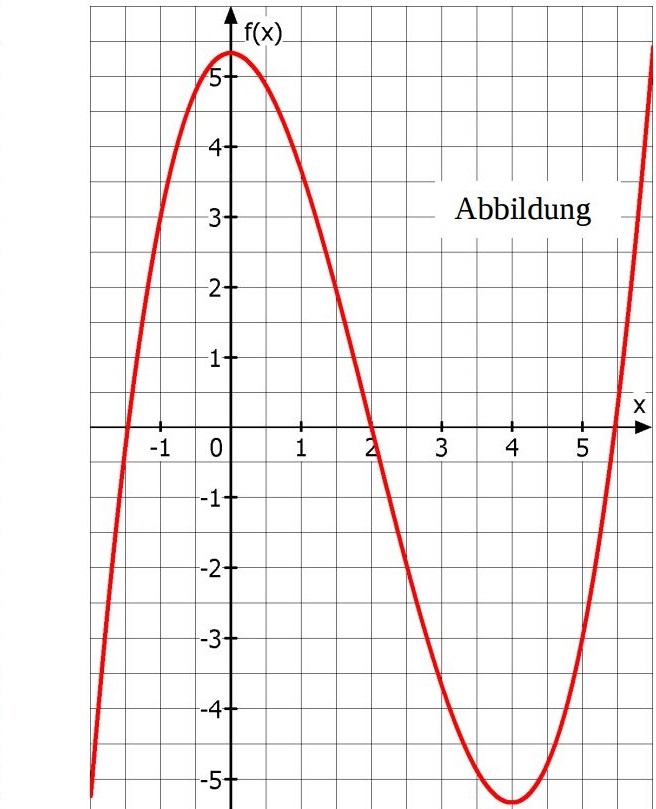
Die folgende Abbildung zeigt den Graphen der Funktion $f(x) = \frac{1}{3}x^3-2x^2+\frac{16}{3}$.
Bestimmen Sie eine Gleichung der Tangente $t$ an den Graphen von $f$ im Punkt P(2$\vert$0).
Skizzieren Sie den Graphen von $f'$ in die Abbildung.
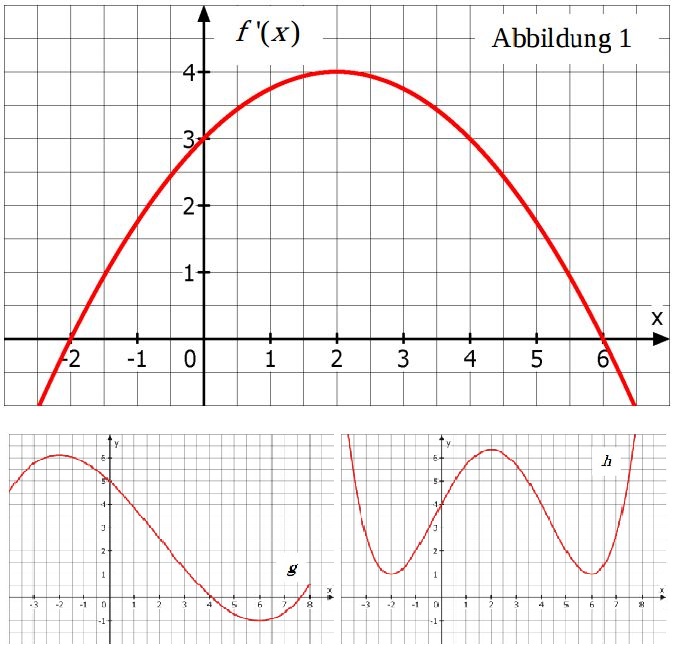
Gegeben ist eine Funktion $f$. Die Abbildung 1 zeigt die Parabel ihrer Ableitungsfunktion $f'(x) = -\frac{1}{4}x^2+x+3$.
Die Parabel von $f'$ besitzt die beiden Nullstellen $x=-2$ und $x=6$. Ermitteln Sie unter Verwendung dieser Nullstellen rechnerisch die Koordinaten des Scheitelpunktes S der Parabel.
Begründen Sie, dass keine der beiden Abbildungen den Graphen der Funktion f zeigt.
Weitere Arbeitsblätter
Ableitungsfunktion und ihre Anwendung
92 min, 12 Aufgaben #1590Aus einer Funktion macht man eine andere Funktion, die sogenannte Ableitungsfunktion. Die Aufgaben beschäftigen sich damit, wie das gemacht wird, und was man darüber hinaus mit der Ableitungsfunktion machen kann. Zum Beispiel Steigungswinkel, Schnittwinkel, Tangentengleichungen oder Berührpunkte bestimmen.
Hemden mit Mängeln Abitur LK Berlin 2011
32 min, 6 Aufgaben #1720Original Abiturprüfung für den Leistungskurs aus Berlin. Die Aufgabe dreht sich rund um Hypothesentests. Kumulierte Binomialverteilung und Standardnormalverteilung, sowie gesunder Menschenverstand werden gebraucht.
Einführung Terme
65 min, 8 Aufgaben #2826Erste Aufgaben zu Termen. Termwerte berechen, Terme vergleichen und Textgleichungen in beide Richtungen: sowohl Gleichungen aus Texten aufstellen aber auch Texte basierend auf Gleichungen verfassen. Die Hälfte der Aufgaben beschäftigt sich mit dem Zusammenfassen von Termen.
Lineare Gleichungen
58 min, 5 Aufgaben #3738Einführung in das Umstellen von linearen Gleichungen. Die Aufgaben beginnen ganz einfach und werden dann nach und nach schwerer. Am Ende hat man gelernt: Klammern auflösen, links und rechts zusammenfassen, alles mit x auf die eine und alles ohne x auf die andere Seite. Zum Schluss noch durch die Zahl vor dem x teilen und fertig ist man.
Binomische Formeln
89 min, 11 Aufgaben #3120Alles rund um die binomischen Formeln. Voraussetzung ist das Auflösen von doppelten Klammern (doppeltes Distributivgesetz). Darauf aufbauend wird auf das Vereinfachen von Termen eingegangen bei denen die binomischen Formeln von einfach bis schwer zur Anwendung kommen. Danach wird der Spieß umgedreht und Terme mit den binomischen Formeln faktorisiert. Krönender Abschluss bilden Gleichungen bei denen man ... *trommelwirbel* ... binomische Formeln braucht.