Einleitung
Originale Arbeit mit 36 erreichbaren Punkten.
24 Minuten Erklärungen in 6 Aufgaben von Koonys Schule.
Aufgaben
Bringe unter eine Wurzel und vereinfache den Radikanden so weit wie möglich.
$8\sqrt{3}$
$4b\sqrt{6b}\cdot\sqrt{3b^4}$, ($b>0$)
Radiziere zunächst so weit wie möglich und vereinfache dann so weit wie möglich.
$6\sqrt{11} - \sqrt{25}\cdot\sqrt{11} + \sqrt{11} - \sqrt{4}\cdot\sqrt{11}$
$\sqrt{1620} - \sqrt{1125} - \sqrt{80}$
Mache den Nenner rational und vereinfache Zähler und Nenner so weit wie möglich.
$\frac{12}{2\sqrt{3}}$
$\frac{2\sqrt{5} + \sqrt{3}}{2\sqrt{5} - \sqrt{3}}$
Vereinfache soweit wie möglich (n$\in\NN$).
$\frac{17^{500}}{17^{200}}$
$7^{2n}\cdot 7^3 \cdot 7^n \cdot 7$
$\left(2^{150}\cdot 9^{150}\right)\cdot (3^{180}\cdot \left(6^{36}\right)^5)$
Vereinfache so weit wie möglich. Im Endergebnis sollen keine negativen Exponenten vorkommen ($x, y, z \in \RR\backslash\{0\}$).
$\left(\frac{2x^8\cdot y^{-3}}{z^5}\right)^2 \cdot \left(\frac{y^2}{x^5\cdot z^{-4}}\right)^3$
Alle Erklärungen sind auch in einer
PDF zum Drucken
Lösungs-PDF
Alle Erklärungen sind auch in einer
Weitere Arbeitsblätter
Flächensätze - Vorwissen I
31 min, 7 Aufgaben #0037Verschiedene grundlegende Aufgaben zu Flächensätze. Der Umgang mit dem für das Thema wichtigen Gleichungen, Flächen- und Winkelberechnungen, sowie erste einfache Aufgaben mit dem Satz des Pythagoras kommen dran.
Übungen zu kombinatorischen Abzählverfahren
29 min, 8 Aufgaben #1648Ob mit oder ohne Reihenfolge und mit oder ohne Wiederholung: die Frage, die sich stellt, ist immer die gleiche: wie viele Möglichkeiten gibt es? Bei den Aufgaben kommt man noch häufig durch Abzählen zur Lösung.
Mathematische Kompetenzen - Zufall
15 min, 6 Aufgaben #0008Ein Sachverhalt aus dem Themengebiet Daten und Zufall (Leitidee 5) wird in verschiedene Aufgaben gepackt, die jeweils einen Schwerpunkt bezüglich der mathematischen Kompetenzen besitzen.
Quadratische Gleichungen
74 min, 7 Aufgaben #0062Es werden zunächst quadratische Gleichungen sowohl über die Scheitelpunktsform als auch mit der pq-Formel gelöst. Im Anschluss gibt es Textaufgaben bei denen das Wissen benötigt wird.
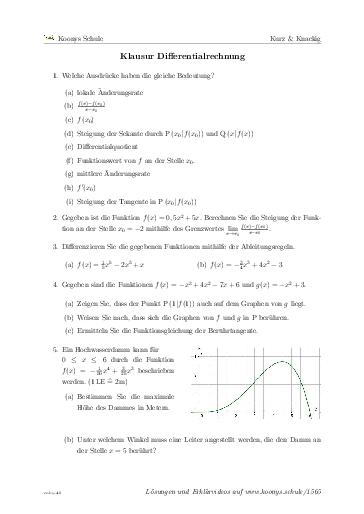
Übungen zur Differenzialrechnung
98 min, 8 Aufgaben #1560Typische Aufgaben zur Differenzialrechnung. Also Ableiten, Nullstellen berechnen, Graphen skizzieren, Tangentengleichungen und Schnittwinkel berechnen und natürlich Hoch- und Tiefpunkte bestimmen.