Einleitung
Erste Aufgaben zu Termen. Termwerte berechen, Terme vergleichen und Textgleichungen in beide Richtungen: sowohl Gleichungen aus Texten aufstellen aber auch Texte basierend auf Gleichungen verfassen.
Die Hälfte der Aufgaben beschäftigt sich mit dem Zusammenfassen von Termen.
65 Minuten Erklärungen in 8 Aufgaben von Koonys Schule.
Aufgaben
Berechne den Wert des Termes und trage die Ergebnisse in die Tabelle ein.
| $x$ | $4 \cdot (x-2)$ |
| 1 | |
| -1 | |
| $\frac{1}{2}$ | |
| $-\frac{1}{2}$ | |
| $-2.5$ |
| $x$ | $x^2 + \frac{3}{4}$ |
| 1 | |
| -1 | |
| $\frac{1}{2}$ | |
| $-\frac{1}{2}$ | |
| $-2.5$ |
| $x$ | $y$ | $y \cdot (3-x)$ |
| 1 | 1 | |
| -1 | 0 | |
| $\frac{1}{2}$ | 1 | |
| $-\frac{1}{2}$ | $\frac{1}{2}$ | |
| $-2.5$ | $-0.5$ |
Stelle jeweils einen Term auf.
Die Hälfte einer Zahl vermindert um 4.
Das Doppelte des Nachfolgers einer natürlichen Zahl.
Vereinfache die Terme soweit wie möglich.
$ 7x + 3 - 2x - 5 $
$ 5a-4+7b -a $
$ -2q + 5p - q^2 + p $
$ 5a^2b - 5ab + 5ab^2 $
$ x^2\cdot x^3 $
$ 7x^3 \cdot (-4x) $
$ 4x+2x^2 - 5x + x^2 - 7y + y $
$ 4x\cdot 2y - 6xy + 3xy : 2 - x $
$ 7xyx^2 - 5x^2\cdot 2xy + 3y\cdot x^3 $
$ \frac{2}{5}p^2q -\frac{1}{5} pq^2 + 4p\cdot 3pq + p $
$ \frac{1}{3} uv - \frac{4}{5} u^2 v + uv - \frac{2}{3}uv\cdot 4u$
Alle Erklärungen sind auch in einer
PDF zum Drucken
Lösungs-PDF
Weitere Arbeitsblätter
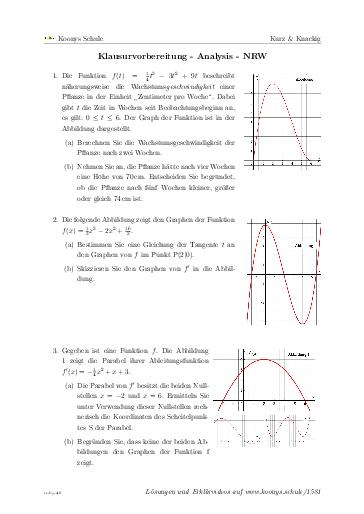
Klausurvorbereitung - Analysis - NRW
16 min, 3 Aufgaben #1581Beispielaufgaben für die zentralen Klausuren aus Nordrhein-Westfalen vom Schulministerium. Es wird vor allem das Verständnis der Ableitungsfunktion geprüft. Wachstumsgeschwindigkeiten, Funktionsgleichungen von Tangenten und Skizzen kommen vor.
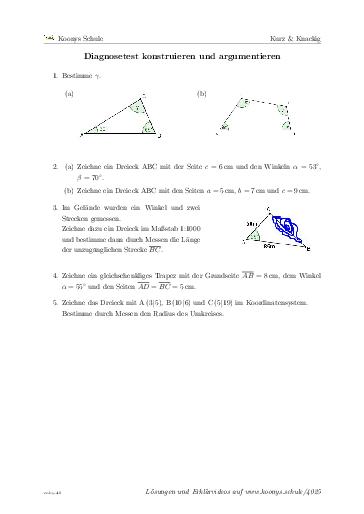
Diagnosetest konstruieren und argumentieren
36 min, 5 Aufgaben #4025Aufgaben zur Konstruktion von Dreiecken mit Hilfe der Kongruenzsätze. Außerdem kommen Innenwinkelsatz, ein gleichschenkliges Trapez und die Konstruktion des Umkreises eines Dreiecks im Koordinatensystem vor.
Klassenarbeit Terme und Gleichungen
26 min, 5 Aufgaben #3750Klassenarbeit einer 8. Klasse auf einem Berliner Gymnasium. Es müssen Terme vereinfacht und Gleichungen gelöst werden. Dabei müssen Klammern aufgelöst, binomische Formeln angewendet und Gleichungen aus Texten aufgestellt werden.
Bernoulli-Ketten
43 min, 4 Aufgaben #1700Es gibt vier grundlegende Aufgabentypen bei Bernoulli-Ketten. Diese werden hier einfach straightforward geübt.
Ikarus Abitur GK Berlin 2016
64 min, 6 Aufgaben #1980Abituraufgabe zur analytischen Geometrie für den Grundkurs mit 30 erreichbaren Bewertungseinheiten aus Berlin 2016.